
分析 (1)根据有理数的加法和减法可以解答本题;
(2)根据有理数的加法和减法可以解答本题;
(3)根据有理数的乘法可以解答本题;
(4)根据有理数的乘法和除法可以解答本题;
(5)根据乘法分配律可以解答本题;
(6)根据有理数的加减法和乘除法可以解答本题.
解答 解:(1)7-(-5)+(-1)
=7+5+(-1)
=11;
(2)5.7+(-0.9)+4.3+(-8.1)
=(5.7+4.3)+[(-0.9)+(-8.1)]
=10+(-9)
=1;
(3)(-4)×4.52×(-2.5)
=4×2.5×4.52
=10×4.52
=45.2;
(4)(-81)÷$\frac{9}{4}$×$\frac{4}{9}$÷(-8)
=81×$\frac{4}{9}×\frac{4}{9}×\frac{1}{8}$
=2;
(5)(-$\frac{1}{2}$-$\frac{1}{3}$+$\frac{3}{4}$)×(-60)
=$-\frac{1}{2}×(-60)-\frac{1}{3}×(-60)+\frac{3}{4}×(-60)$
=30+20-45
=5;
(6)-52-[-4+(1-0.2×$\frac{1}{5}$)÷(-2)]
=-25-[-4+(1-$\frac{1}{25}$)×$(-\frac{1}{2})$]
=-25-[-4-$\frac{12}{25}$]
=-25+4+$\frac{12}{25}$
=-20$\frac{13}{20}$.
点评 本题考查有理数的混合运算,解题的关键是明确有理数混合运算的计算方法.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
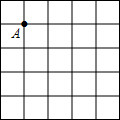 如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.
如图,在5×5的正方形网格中,每个小正方形的边长为1,请在所给网格中按下列要求画出图形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
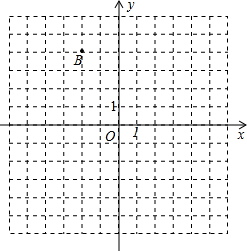 如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.
如图在直角坐标平面内,已知点A(-2,-3)与点B,将点A向右平移7个单位到达点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
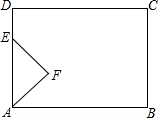 如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).
如图,在矩形ABCD中,AB=8cm,BC=6cm,动点E从点A出发.以2cm/s的速度沿射线AD方向运动,以AE为底边,在AD的右侧作等腰直角角形AEF,当点F落在射线BC上时,点E停止运动,设△AEF与矩形ABCD重叠部分的面积为S,运动的时间为t(s).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com