
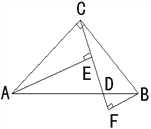
【题目】如图,已知:AC=BC,AC⊥BC,AE⊥CF,BF⊥CF,C、E、F分别为垂足, 且∠BCF=∠ABF,CF交AB于D.
(1)判断△BCF≌△CAE,并说明理由.
(2)判断△ADC是不是等腰三角形?并说明理由.
【答案】(1)△BCF≌△CAE.理由见解析;
(2)△ADC是等腰三角形.理由见解析.
【解析】(1)解:△BCF≌△CAE.理由如下:
∵AC⊥BC,AE⊥CF,
∴∠ACE+∠BCF=90°,∠ACE+∠CAE=90°,
∴∠CAE=∠BCF,
∵AE⊥CF,BF⊥CF,
∴∠AEC=∠F=90°,
在△BCF和△CAE中,
∵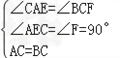 ,
,
∴△BCF≌△CAE(AAS);
(2)解:△ADC是等腰三角形.理由如下:
∵AC⊥BC,BF⊥CF,
∴∠ACB=∠F=90°,
∴∠ACD+∠BCF=90°,∠BDF+∠ABF=90°,
∵∠BCF=∠ABF,
∴∠ACD=∠BDF,
又∵∠BDF=∠ADC(对顶角相等),
∴∠ACD=∠ADC,
∴AC=AD,
故△ADC是等腰三角形。


 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系上有个点P(1,0),点P第一次向上跳运1个单位至P1(1,1),紧接着第二次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第100次跳动至点P100的坐标是( )
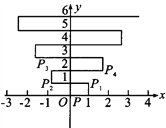
A. (-24,49) B. (-25,50) C. (26,50) D. (26,51)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商品原价800元,连续两次降价a%后售价为578元,下列所列方程正确的是( )
A. 800(1+a%)2=578 B. 800(1-a%)2="578" C. 800(1-2a%)=578 D. 800(1-a2%)=578
查看答案和解析>>
科目:初中数学 来源: 题型:
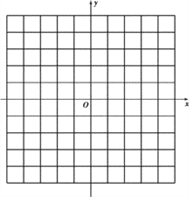
【题目】如图所示的方格纸中每个小方格都是边长为1个单位长度的正方形,建立如图所示的平面直角坐标系,已知点A(1,0),B(4,0),C(3,3),D(1,4)
(1) 描出A、B、C、D、四点的位置,并顺次连接ABCD,
(2) 四边形ABCD的面积是________.
(3) 把四边形ABCD向左平移5个单位,再向下平移2个单位得到四边形A'B'C'D',写出点A'、B'、C'、D'的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com