如图，正方形ABCD的边长是2，M是AD的中点．
点E从点A出发，沿AB运动到
点B停止．连接EM并延长交射线CD于点F，过M作EF的垂线交射线BC于点G，连接EG、FG．
（1）设AE=x时，△EGF的面积为y．求y关于x的函数关系式，
并写出自变量x的取值范围；
（2）P是MG的中点，求点P运动路线的长．
科目：初中数学 来源： 题型：
学生的上学方式是初中生生活自理能力的一种反映．为此，怀柔区某初三数学老师组织本班学生，运用他们所学的统计知识，对初一学生上学的四种方式：骑车、步行、乘车、接送，进行抽样调查，并将调查的结果绘制成图（1）、图（2）．请根据图中提供的信息，解答下列问题：
(1)抽样调查的样本容量为________，其中步行人数占样本容量的_____%，骑车人数占样本容量的_____%．
(2)请将图（1）补充完整．
(3)根据抽样调查结果，你估计该校初一年级800名学生中，大约有多少名学生是由家长接送上学的？
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
如图，正三角形ABC、正四边形ABCM、正五边形ABCMN中，点E在CB的延长线
上，点D在另一边反向延长线上，且BE=CD，DB延长线交AE于点F．
图1中∠AFB的度数为 ，图2中∠
AFB度数为 ， 若将条件“正三角形、
正四边形、正五边形”改为“正n边形”，其它条件不变，则∠AFB度数为 ．
（用含n的代数式表示）
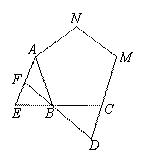
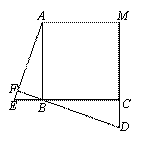
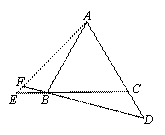
图1 图2 图3
查看答案和解析>>
科目：初中数学 来源： 题型：
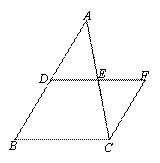
如图，在△ABC中，D、E分别是AB、AC的中点，延长DE到点F，使EF＝DE，连接CF．
（1）求证: 四边形BCFD是平行四边形；
（2）若BD=4，BC=6，∠F=60°，求CE的长.
查看答案和解析>>
科目：初中数学 来源： 题型：
为了解居民用水情况，晓娜在某小区随机抽查了10户家庭的月用水量，结果如下表：
| 月用水量（吨） | 5 | 6 | 7 | 8 | 9 | 10 |
| 户数 | 1 | 1 | 2 | 2 | 3 | 1 |
则这10户家庭的月用水量的平均数和众数分别是
A．7.8，9 B．7.8
，3 C．4.5，9 D．4.5，3
查看答案和解析>>
科目：初中数学 来源： 题型：
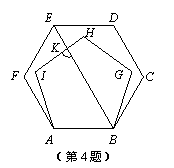
把边长相等的正五边形ABGHI和正六边形ABCDEF的AB边重合，按照如图的方式叠合在一起，连接EB，交HI于点K，则∠BKI的大小为
 |
| A．90° | B．84° |
| C．72° | D．88° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，那么这个正多边形的边数是（ ）
．