
����Ŀ�������������˵���� 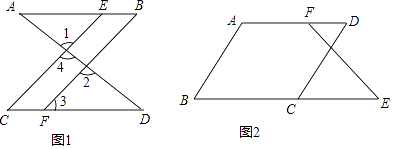
��1����ͼ1����֪��1=��2����B=��C�����Ƴ�AB��CD���������£� ��Ϊ��1=��2����֪�����ҡ�1=��4����
���ԡ�2=��4������������
����CE��BF����
���ԡ�=��3����
����Ϊ��B=��C����֪��
���ԡ�3=��B������������
����AB��CD����
��2����ͼ2����֪��B+��BCD=180�㣬��B=��D����֤����E=��DFE�� ֤�����ߡ�B+��BCD=180�㣨��֪����
��AB��CD ����
���B=����
�֡ߡ�B=��D����֪����
���=��������������
��AD��BE����
���E=��DFE����
���𰸡�
��1���Զ�����ȣ�ͬλ����ȣ���ֱ��ƽ�У�C����ֱ��ƽ�У�ͬλ����ȣ��ڴ�����ȣ���ֱ��ƽ��
��2��ͬ���ڽǻ�������ֱ��ƽ�У���DCE����ֱ��ƽ�У�ͬλ����ȣ�DCE��D���ڴ�����ȣ���ֱ��ƽ�У���ֱ��ƽ�У��ڴ������
���������⣺��1�����ɣ���Ϊ��1=��2����֪�����ҡ�1=��4���Զ�����ȣ��� ���ԡ�2=��4������������������CE��BF��ͬλ����ȣ���ֱ��ƽ�У������ԡ�C=��3����ֱ��ƽ�У�ͬλ����ȣ�������Ϊ��B=��C����֪�������ԡ�3=��B������������������AB��CD���ڴ�����ȣ���ֱ��ƽ�У������Դ��ǣ��Զ�����ȣ�ͬλ����ȣ���ֱ��ƽ�У�C����ֱ��ƽ�У�ͬλ����ȣ��ڴ�����ȣ���ֱ��ƽ�У���2��֤�����ߡ�B+��BCD=180�㣨��֪������AB��CD ��ͬ���ڽǻ�������ֱ��ƽ�У������B=��DCE����ֱ��ƽ�У�ͬλ����ȣ����֡ߡ�B=��D����֪����
���DCE=��D ����������������AD��BE���ڴ�����ȣ���ֱ��ƽ�У������E=��DFE����ֱ��ƽ�У��ڴ�����ȣ������Դ��ǣ�ͬ���ڽǻ�������ֱ��ƽ�У���DCE����ֱ��ƽ�У�ͬλ����ȣ�DCE��D���ڴ�����ȣ���ֱ��ƽ�У���ֱ��ƽ�У��ڴ�����ȣ�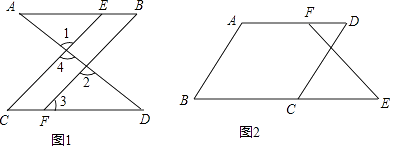
�����㾫��������ƽ���ߵ��ж������ʶ���Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪�ɽǵ���Ȼ���������ϵ�����������õ�����ֱ��ƽ�У�λ�ù�ϵ������ƽ���ߵ��ж�����ƽ���ߣ�λ�ù�ϵ���õ��йؽ���Ȼ���������ϵ���Ľ�����ƽ���ߵ����ʣ�


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������10����+10�ף���ô������20������ ��
A.20��
B.��20��
C.10��
D.��10��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ���������У�����һ���������һ����ǵ�2�����������������С�Ľ��ǣ�������
A.15��
B.30��
C.60��
D.90��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijͬѧ�ڼ���һ������ʽ������3x2ʱ����������ţ�����˼�����3x2���õ��Ľ����x2��4x+1����ô��ȷ�ļ������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ж���ʽ��˵Ľ����a2-a-6���ǣ� ��
A����a-2����a+3�� B����a+2����a-3�� C����a-6����a+1�� D����a+6����a-1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ij������������16�棬�������Ϊ��2�棬��õ���һ����²��ǣ� ��
A.��18��
B.��14��
C.14��
D.18��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����κ���y=ax2+bx+c��a��0����ͼ����ͼ�����������ĸ����ۣ���4ac��b2��0����4a+c��2b����3b+2c��0����m��am+b��+b��a��m�٩�1����������ȷ���۵ĸ����ǣ�����
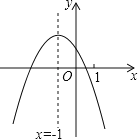
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��������A�ؿ���B�أ�һ��С������B�ؿ���A�أ�ͬʱ��������������ʻ�����Ե����յ��ֹͣ���������С����֮��ľ���Ϊs��ǧ�ף���������ʻ��ʱ��Ϊt��Сʱ����S��t֮��ĺ�����ϵ��ͼ��ʾ������˵������ȷ���У� ��
��A��B�������60ǧ�ף�
������1Сʱ��������С����������
��С�������ٶ��ǻ����ٶȵ�2����
������1.5Сʱ��С�����Ȼ�������ʻ��60ǧ�ף�
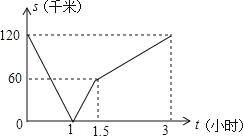
A��1�� B��2�� C��3�� D��4��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com