
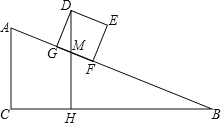
【题目】某仓储中心有一个坡度为i=1:2的斜坡AB,顶部A处的高AC为4米,B、C在同一水平地面上,其横截面如图.
(1)求该斜坡的坡面AB的长度;
(2)现有一个侧面图为矩形DEFG的长方体货柜,其中长DE=2.5米,高EF=2米,该货柜沿斜坡向下时,点D离BC所在水平面的高度不断变化,求当BF=3.5米时,点D离BC所在水平面的高度DH.
 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】合与实践﹣﹣探究图形中角之间的等量关系及相关问题.
问题情境:
正方形ABCD中,点P是射线DB上的一个动点,过点C作CE⊥AP于点E,点Q与点P关于点E对称,连接CQ,设∠DAP=α(0°<α<135°),∠QCE=β.
初步探究:
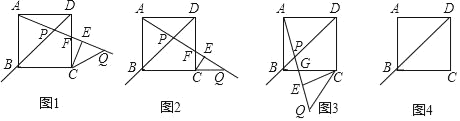
(1)如图1,为探究α与β的关系,勤思小组的同学画出了0°<α<45°时的情形,射线AP与边CD交于点F.他们得出此时α与β的关系是β=2α.借助这一结论可得当点Q恰好落在线段BC的延长线上(如图2)时,α= °,β= °;
深入探究:
(2)敏学小组的同学画出45°<α<90°时的图形如图3,射线AP与边BC交于点G.请猜想此时α与β之间的等量关系,并证明结论;
拓展延伸:
(3)请你借助图4进一步探究:①当90°<α<135°时,α与β之间的等量关系为 ;
②已知正方形边长为2,在点P运动过程中,当α=β时,PQ的长为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某区在实施居民用水管理前,随机调查了部分家庭(单位:户)去年的月均用水量(单位:t),并将调查数据进行整理,绘制出如下不完整的统计图表:
月均用水量 | 频数 | 频率 |
0≤x<5 | 6 | 12% |
5≤x<10 | 12 | 24% |
10≤x<15 |
| 32% |
15≤x<20 | 10 | 20% |
20≤x<25 | 4 |
|
25≤x<30 | 2 | 4% |
合计 |
| 100% |
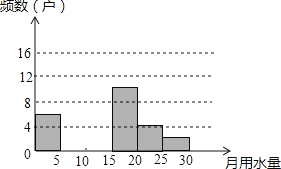
请解答以下问题:
(I)把上面的频数分布表和频数分布直方图补充完整;
(Ⅱ)若该小区有2000户家庭,根据此次随机抽查的数据估计,该小区月均用水量不低于20t的家庭有多少户?
(Ⅲ)为了鼓励节约用水,要确定一个月均用水量的标准,超出该标准的部分按1.5倍价格收费,若要使68%的家庭水费支出不受影响,那么,你觉得家庭月均用水量应定为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
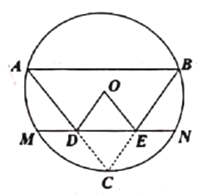
【题目】如图,在△ABC中,AC=BC=5, AB=6, 点D为AC上一点,作DE//AB交BC于点E,点C关于DE的对称点为点O,以OA为半径作⊙O恰好经过点C,并交直线DE于点M,N.则MN的值为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一元二次方程mx2-2mx+m-2=0.
(1)若方程有两个不等实数根,求m的取值范围;
(2)若方程的两实数根为x1,x2,且|x1-x2|=1,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形![]() 为
为![]() 的内接四边形,直径
的内接四边形,直径![]() 与对角线
与对角线![]() 相交于点
相交于点![]() ,作
,作![]() 于
于![]() ,
,![]() 与过
与过![]() 点的直线相交于点
点的直线相交于点![]() ,
,![]() .
.
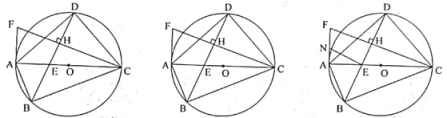
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
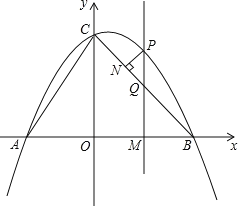
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .点
.点![]() 是第一象限内抛物线上的一个动点,点
是第一象限内抛物线上的一个动点,点![]() 的横坐标为
的横坐标为![]() .
.
(1)求此抛物线的表达式;
(2)过点![]() 作
作![]() 轴,垂足为点
轴,垂足为点![]() ,
,![]() 交
交![]() 于点
于点![]() .试探究点P在运动过程中,是否存在这样的点
.试探究点P在运动过程中,是否存在这样的点![]() ,使得以
,使得以![]() 为顶点的三角形是等腰三角形.若存在,请求出此时点
为顶点的三角形是等腰三角形.若存在,请求出此时点![]() 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .请用含
.请用含![]() 的代数式表示线段
的代数式表示线段![]() 的长,并求出当
的长,并求出当![]() 为何值时
为何值时![]() 有最大值,最大值是多少?
有最大值,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
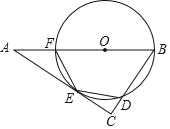
【题目】如图,点O是△ABC的边AB上一点,⊙O与边AC相切于点E,与边BC,AB分别相交于点D,F,且DE=EF.
(1)求证:∠C=90°;
(2)当BC=3,sinA=![]() 时,求AF的长.
时,求AF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com