
【题目】问题情境:如图1,AB∥CD, ![]() ,
,![]() .求
.求![]() 度数.
度数.
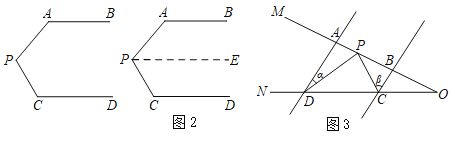
小明的思路是:如图2,过P作PE∥AB,通过平行线性质,可得![]() _______.
_______.
问题迁移:如图3,AD∥BC,点P在射线OM上运动, ![]() ,
, ![]() .
.
(1)当点P在A、B两点之间运动时, ![]() 、
、![]() 、
、![]() 之间有何数量关系?请说明理由.
之间有何数量关系?请说明理由.
(2)如果点P在A、B两点外侧运动时(点P与点A、B、O三点不重合),请你直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
【答案】![]() ;
;
(1)![]() ,理由见解析;
,理由见解析;
(2)当点P在B、O两点之间时, ![]() ;
;
当点P在射线AM上时, ![]() .
.
【解析】试题分析:(1)过P作PE∥AB,通过平行线性质求∠APC即可;(2)过P作PE∥AD交CD于E,推出AD∥PE∥BC,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案;(3)画出图形,根据平行线的性质得出∠α=∠DPE,∠β=∠CPE,即可得出答案.
试题解析:(1)过点P作PE∥AB,
∵AB∥CD,
∴PE∥AB∥CD,
∴∠A+∠APE=180°,∠C+∠CPE=180°,
∵∠PAB=130°,∠PCD=120°,
∴∠APE=50°,∠CPE=60°,
∴∠APC=∠APE+∠CPE=110°.
故答案为110°.
(1)过P作PQ∥AD.

∵AD∥BC,
∴AD∥PQ ,
PQ∥BC
∵PQ∥AD,
∴![]()
同理, ![]()
∴![]()
(2)(3)当P在BA延长线时,

∠CPD=∠β∠α;
当P在AB延长线时,

∠CPD=∠α∠β.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=1,△A'B'C是由△ABC绕点C顺时针旋转所得,连接AB',且点A,B',A'在同一条直线上,则AA'的长为__.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,BC=a,AC=b,AB=c,若∠C=90°,如图(1),根据勾股定理,则a2+b2=c2,若△ABC不是直角三角形,如图(2)和图(3),请你类比勾股定理,试猜想a2+b2与c2的关系,并证明你的结论.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮早晨从家骑车到学校,先上坡后下坡,所行路程y(米)与时间x(分钟)的关系如图所示,若返回时上坡、下坡的速度仍与去时上、下坡的速度分别相同,则小明从学校骑车回家用的时间是________分钟.
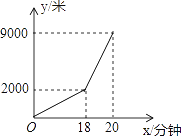
查看答案和解析>>
科目:初中数学 来源: 题型:
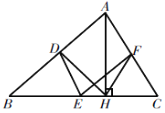
【题目】如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.
(1)试判断线段DE与FH之间的数量关系,并说明理由;
(2)求证:∠DHF=∠DEF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠1+∠2=180°,∠3=∠B,试说明DE∥BC.下面是部分推导过程,请你在括号内填上推导依据或内容:
证明:∵∠1+∠2=180°(已知)
∠1=∠4 ( )
∴∠2+∠4=180°(等量代换)
∵EH∥AB( )
∴∠B= ( )
∵∠3=∠B(已知)
∴∠3=∠EHC(等量代换)
∴DE∥BC ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年中考前,张老师为了解全市初三男生体育考试项目的选择情况(每人限选一项),在全市范围内随机调查了部分初三男生,将调查结果分成五类:A.推实心球(2kg);B.立定跳远;C.半场运球;D.跳绳;E.其他,并将调查结果绘制成以下两幅不完整的统计图,请你根据统计图解答下列问题: 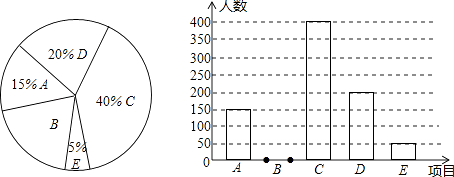
(1)将上面的条形统计图补充完整;
(2)假定全市初三毕业学生中有32000名男生,试估计全市初三男生中选半场运球的人数有多少人;
(3)甲、乙两名初三男生在上述选择率较高的三个项目:B.立定跳远;C.半场运球;D.跳绳中各选一项,同时选择半场运球、立定跳远的概率是多少?请用列表法或画树形图的方法加以说明并列出所有等可能的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】邻边不相等的平行四边形纸片,剪去一个菱形,余下的一个四边形,称为第一次操作;在余下的四边形纸片中再剪去一个菱形,又余下一个四边形,称为第二次操作;…依此类推,若第n次操作余下的四边形是菱形,则称原平行四边形为n阶准菱形,如图1,ABCD中,若AB=1,BC=2,则ABCD为1阶准菱形.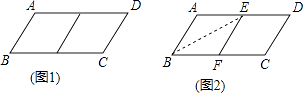
(1)猜想与计算:
邻边长分别为3和5的平行四边形是阶准菱形;已知ABCD的邻边长分别为a,b(a>b),满足a=8b+r,b=5r,请写出ABCD是阶准菱形.
(2)操作与推理:
小明为了剪去一个菱形,进行了如下操作:如图2,把ABCD沿BE折叠(点E在AD上),使点A落在BC边上的点F处,得到四边形ABFE.请证明四边形ABFE是菱形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com