
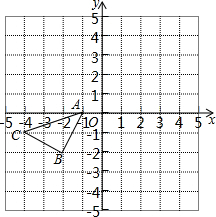
 如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,请在所给直角坐标系中按要求画图和解答下列问题:分析 (1)利用网格特点和旋转的性质画出点B、C的对应点B1、C1,则可得到△AB1C1;
(2)根据关于原点对称的点的坐标特征写出点A2、B2、C2的坐标,然后描点即可得到△A2B2C2;
(3)先利用关于x轴的对称点的坐标特征写出P点坐标,再描点得到P点,然后观察图形可判断x的取值范围.
解答 解:(1)如图,△AB1C1为所作;
(2)如图,△A2B2C2.为所作;
(3)如图,点P为所作;x的取值范围为5.5<x<8.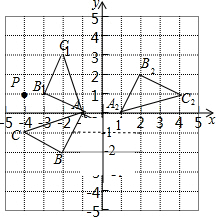
点评 本题考查了作图-旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.也考查了平移变换.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种消毒液(瓶) | 乙种消毒液(瓶) | 总费用(元) | |
| 第一次 | 40 | 60 | 660 |
| 第二次 | 80 | 30 | 690 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
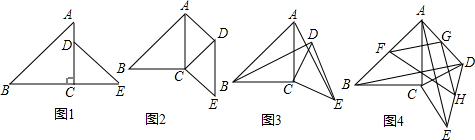 问题情境:
问题情境:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 购买一种水果,所付款金额(元)与购买数量(千克)之间的函数图象由线段OA和射线AB组成,如图所示,则一次购买20千克这种水果,比分两次每次购买10千克这种水果可以节省的费用为( )
购买一种水果,所付款金额(元)与购买数量(千克)之间的函数图象由线段OA和射线AB组成,如图所示,则一次购买20千克这种水果,比分两次每次购买10千克这种水果可以节省的费用为( )| A. | 20元 | B. | 12元 | C. | 10元 | D. | 8元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,平行四边形中,AE⊥BC于E,AF⊥CD于F.
如图,平行四边形中,AE⊥BC于E,AF⊥CD于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com