
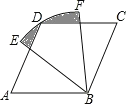
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形EBF的半径为2,圆心角为60°,则图中阴影部分的面积是_____.
【答案】![]()
【解析】
连接BD,易证△DAB是等边三角形,即可求得△ABD的高为![]() ,再证明△ABG≌△DBH,即可得四边形GBHD的面积等于△ABD的面积,由图中阴影部分的面积为S扇形EBF﹣S△ABD即可求解.
,再证明△ABG≌△DBH,即可得四边形GBHD的面积等于△ABD的面积,由图中阴影部分的面积为S扇形EBF﹣S△ABD即可求解.
如图,连接BD.

∵四边形ABCD是菱形,∠A=60°,
∴∠ADC=120°,
∴∠1=∠2=60°,
∴△DAB是等边三角形,
∵AB=2,
∴△ABD的高为![]() ,
,
∵扇形BEF的半径为2,圆心角为60°,
∴∠4+∠5=60°,∠3+∠5=60°,
∴∠3=∠4,
设AD、BE相交于点G,设BF、DC相交于点H,
在△ABG和△DBH中,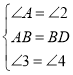 ,
,
∴△ABG≌△DBH(ASA),
∴四边形GBHD的面积等于△ABD的面积,
∴图中阴影部分的面积是:S扇形EBF﹣S△ABD=![]() ﹣
﹣![]() ×2×
×2×![]() =
=![]() .
.
故答案是:![]() .
.


 新思维假期作业寒假吉林大学出版社系列答案
新思维假期作业寒假吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】反比例函数![]() 在第一象限的图象如图所示,过
在第一象限的图象如图所示,过![]() 上任意一点
上任意一点![]() ,作
,作![]() 轴垂线交
轴垂线交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,作
,作![]() 轴垂线,交
轴垂线,交![]() 于点
于点![]() ,交
,交![]() 轴于点
轴于点![]() ,直线
,直线![]() 分别交
分别交![]() 轴,
轴,![]() 轴于点
轴于点![]() ,则
,则![]() __________.
__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形的直角顶点在坐标原点,∠OAB=30°,若点A在反比例函数y=![]() (x>0)的图象上,则经过点B的反比例函数解析式为( )
(x>0)的图象上,则经过点B的反比例函数解析式为( )

A. y=﹣![]() B. y=﹣
B. y=﹣![]() C. y=﹣
C. y=﹣![]() D. y=
D. y=![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE=α(0°<α≤90°),点F,G,P分别是DE,BC,CD的中点,连接PF,PG.
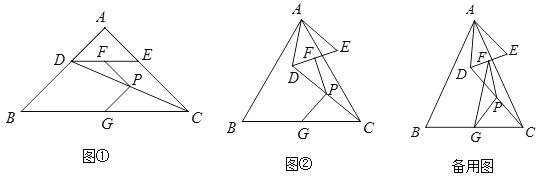
(1)如图①,α=90°,点D在AB上,则∠FPG= °;
(2)如图②,α=60°,点D不在AB上,判断∠FPG的度数,并证明你的结论;
(3)连接FG,若AB=5,AD=2,固定△ABC,将△ADE绕点A旋转,当PF的长最大时,FG的长为 (用含α的式子表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
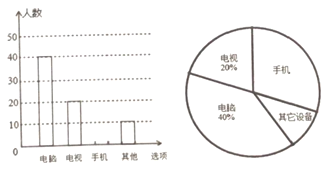
【题目】受疫情影响,很多学校都纷纷响应了“停课不停学”的号召,开展线上教学活动.为了解学生上网课使用的设备类型,某校从“电脑、手机、电视、其它”四种类型的设备对学生做了一次抽样调查.调查结果显示,每个学生只选择了以上四种设备类型中的一种,现将调查的结果绘制成如下两幅不完整的统计图,请你根据图中提供的信息,解答下列问题:
(1)补全条形统计图;
(2)若该校共有1500名学生,估计全校用手机上网课的学生共有___________名;
(3)在上网课时,老师在A、B、C、D四位同学中随机抽取一名学生回答问题,求两次都抽取到同一名学生回答问题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1:![]() ,AB=10米,AE=15米.(i=1:
,AB=10米,AE=15米.(i=1:![]() 是指坡面的铅直高度BH与水平宽度AH的比)
是指坡面的铅直高度BH与水平宽度AH的比)

(1)求点B距水平面AE的高度BH;
(2)求广告牌CD的高度.
(测角器的高度忽略不计,结果精确到0.1米.参考数据:![]() 1.414,
1.414,![]() 1.732)
1.732)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象交反比例函数y=![]() (x>0)的图象于点A、B,交x轴于点C.
(x>0)的图象于点A、B,交x轴于点C.
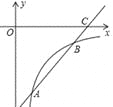
(1)求m的取值范围;
(2)若点A的坐标是(2,-4),且![]() =
=![]() ,求m的值和一次函数的解析式.
,求m的值和一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面内有一等腰直角三角板(∠ACB=90°)和一直线MN,过点C作CE⊥MN于点E,过点B作BF⊥MN于点F.当点E与点A重合时(如图①),易证:AF+BF=2CE;当三角板绕点A顺时针旋转至图②、图③的位置时,上述结论是否仍然成立?若成立,请给予证明;若不成立,线段AF、BF、CE之间又有怎样的数量关系,请直接写出你的猜想,请直接写出你的猜想,不需证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度![]() (米/分钟)与时间
(米/分钟)与时间![]() (分钟)前2分钟满足二次函数
(分钟)前2分钟满足二次函数![]() ,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.
,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.
(1)求第一颗弹珠的速度![]() (米/分钟)与时间
(米/分钟)与时间![]() (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度![]() (米/分钟)与弹出第一颗弹珠后的时间
(米/分钟)与弹出第一颗弹珠后的时间![]() (分钟)之间的函数关系式;
(分钟)之间的函数关系式;
(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;
(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com