Question

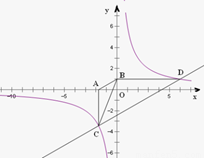
如图，已知双曲线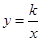经过点D（6，1），点C是双曲线第三象限分支上的动点，过C作CA⊥x轴，过D作DB⊥y轴，垂足分别为A，B，连接AB，BC.

（1）求k的值；

（2）若△BCD的面积为12，求直线CD的解析式；

（3）判断AB与CD的位置关系，并说明理由.

 

Answer 1

【答案】

（1）k=6；（2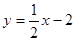）；（3）根据题意求出点A、B的坐标，然后利用待定系数法求出直线AB的解析式，可知与直线CD的解析式k值相等，所以AB、CD平行．

【解析】

试题分析：（1）把点D的坐标代入双曲线解析式，进行计算即可得解；

（2）先根据点D的坐标求出BD的长度，再根据三角形的面积公式求出点C到BD的距离，然后求出点C的纵坐标，再代入反比例函数解析式求出点C的坐标，然后利用待定系数法求一次函数解析式解答；

（3）根据题意求出点A、B的坐标，然后利用待定系数法求出直线AB的解析式，可知与直线CD的解析式k值相等，所以AB、CD平行．

解：（1）∵双曲线经过点D（6，1），

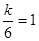∴，解得k=6；

（2）设点C到BD的距离为h，

∵点D的坐标为（6，1），DB⊥y轴，

∴BD=6，

∴S_△BCD=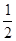×6•h=12，

解得h=4，

∵点C是双曲线第三象限上的动点，点D的纵坐标为1，

∴点C的纵坐标为1-4=-3，

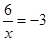∴，解得x=-2，

∴点C的坐标为（-2，-3），

设直线CD的解析式为y=kx+b，

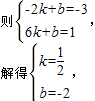
所以，直线CD的解析式为；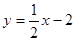

（3）AB∥CD．理由如下：

∵CA⊥x轴，DB⊥y轴，设点C的坐标为（c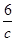，），点D的坐标为（6，1），

∴点A、B的坐标分别为A（c，0），B（0，1），

设直线AB的解析式为y=mx+n，

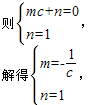
所以，直线AB的解析式为y=-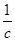x+1，

设直线CD的解析式为y=ex+f，

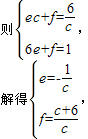
∴直线CD的解析式为y=-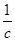x+，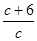

∵AB、CD的解析式k都等于-，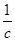

∴AB与CD的位置关系是AB∥CD．

考点：反比例函数的综合题

点评：本题是对反比例函数的综合考查，主要利用了待定系数法求函数解析式，三角形的面积的求解，待定系数法是求函数解析式最常用的方法，一定要熟练掌握并灵活运用．