
【题目】对任意一个三位数n,如果n满足各个数位上的数字互不相同,且都不为零,那么称这个数为“相异数”,将一个“相异数”任意两个数位上的数字对调后可以得到三个不同的新三位数,把这三个新三位数的和与111的商记为F(n).例如n=123,对调百位与十位上的数字得到213,对调百位与个位上的数字得到321,对调十位与个位上的数字得到132,这三个新三位数的和为213+321+132=666,666÷111=6,所以F(123)=6.
(1)计算:F(243),F(617);
(2)若s,t都是“相异数”,其中s=100x+32,t=150+y(1≤x≤9,1≤y≤9,x,y都是正整数),规定:k= ![]() ,当F(s)+F(t)=18时,求k的最大值.
,当F(s)+F(t)=18时,求k的最大值.
【答案】
(1)解:F(243)=(423+342+234)÷111=9;
F(617)=(167+716+671)÷111=14.
(2)解:∵s,t都是“相异数”,s=100x+32,t=150+y,
∴F(s)=(302+10x+230+x+100x+23)÷111=x+5,F(t)=(510+y+100y+51+105+10y)÷111=y+6.
∵F(t)+F(s)=18,
∴x+5+y+6=x+y+11=18,
∴x+y=7.
∵1≤x≤9,1≤y≤9,且x,y都是正整数,
∴ ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() 或
或 ![]() .
.
∵s是“相异数”,
∴x≠2,x≠3.
∵t是“相异数”,
∴y≠1,y≠5.
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴ ![]() 或
或 ![]() 或
或 ![]() ,
,
∴k的最大值为 ![]() .
.
【解析】(1)根据F(n)的定义式,分别将n=243和n=617代入F(n)中,即可求出结论;(2)由s=100x+32、t=150+y结合F(s)+F(t)=18,即可得出关于x、y的二元一次方程,解之即可得出x、y的值,再根据“相异数”的定义结合F(n)的定义式,即可求出F(s)、F(t)的值,将其代入k= ![]() 中,找出最大值即可.
中,找出最大值即可.


科目:初中数学 来源: 题型:
【题目】2016年9月10日,郑徐高铁正式运营.从徐州到郑州全程约360km,高铁开通后,运行时间比特快列车所用的时间减少了2.1小时.若高铁列车的平均速度是特快列车平均速度的2.4倍,求特快列车的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AD=4,点E是对角线AC上一点,连接DE,过点E作EF⊥ED,交AB于点F,连接DF,交AC于点G,将△EFG沿EF翻折,得到△EFM,连接DM,交EF于点N,若点F是AB的中点,则△EMN的周长是 . 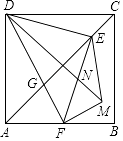
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表列出了国外几个城市与首都北京的时差(带正号的表示同一时刻比北京时间早的时数),如北京时间的上午10:00时,东京时间的10点已过去了1小时,现在已是10+1=11:00.

(1)如果现在是北京时间8:00,那么现在的纽约时间是多少;
(2)此时(北京时间8:00)小明想给远在巴黎姑妈打电话,你认为合适吗?为什么?
(3)如果现在是芝加哥时间上午6:00,那么现在北京时间是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,隧道的截面由半圆和长方形构成,长方形的长BC为8m,宽AB为1m,该隧道内设双向行驶的车道(共有2条车道),若现有一辆货运卡车高4m,宽2.3m。则这辆货运卡车能否通过该隧道?说明理由.
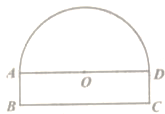
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,已知点C在线段AB上,且AC=5cm,BC=3cm,点M,N分别是AC,BC的中点,求线段MN的长度.
(2)若点C是线段AB上任意一点,且AC=a,BC=b, 点M、N分别是,AC,BC的中点,请直接写出线段MN的长度(用含a,b的代数式表示)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将含45°角的三角板的直角顶点R放在直线l上,分别过两锐角的顶点M,N作l的垂线,垂足分别为P、Q,
(1)如图1,观察图1可知:与NQ相等的线段是 , 与∠NPQ相等的角是 . 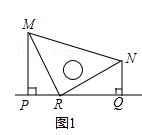
(2)直角△ABC中,∠B=90°,在AB边上任取一点D,连接CD,分别以AC,DC为边作正方形ACEF和正方形CDGH,如图2,过E,H分别作BC所在直线的垂线,垂足分别为K,L.试探究EK与HL之间的数量关系,并证明你的结论.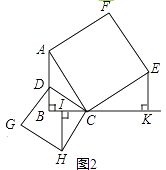
(3)直角△ABC中,∠B=90°,在AB边上任取一点D,连接CD,分别以AC,DC为边作矩形ACEF和矩形CDGH,连接EH交BC所在的直线于点T,如图3,如果AC=kCE,CD=kCH,试探究TE与TH之间的数量关系,并证明你的结论.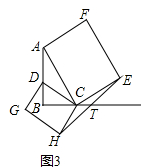
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com