
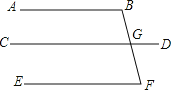
【题目】如图:已知∠B=∠BGD,∠DGF=∠F,求证:∠B+∠F=180°.
请你认真完成下面的填空.
证明:∵∠B=∠BGD ( 已知 )
∴AB∥CD ( )
∵∠DGF=∠F;( 已知 )
∴CD∥EF ( )
∴AB∥EF ( )
∴∠B+∠F=180°( ).
【答案】内错角相等,两直线平行;内错角相等,两直线平行;平行于同一条直线的两条直线平行;两直线平行,同旁内角互补.
【解析】
观察图形,由∠B=∠BGD,根据内错角相等,两直线平行,即可证得AB∥CD,又由∠DGF=∠F,根据内错角相等,两直线平行,可证得CD∥EF,由平行于同一条直线的两条直线平行,则得AB∥EF,再根据两直线平行 同旁内角互补,易得∠B+∠F=180°.
证明:∵∠B=∠BGD(已知),
∴AB∥CD(内错角相等,两直线平行),
∵∠DGF=∠F(已知),
∴CD∥EF(内错角相等,两直线平行),
∴AB∥EF(平行于同一条直线的两条直线平行)
∴∠B+∠F=180°(两直线平行,同旁内角互补);
故答案为:内错角相等,两直线平行;内错角相等,两直线平行;平行于同一条直线的两条直线平行;两直线平行,同旁内角互补.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】综合探究:如图1,在平面直角坐标系xOy中,抛物线y=﹣![]() +bx+8与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE、EC.
+bx+8与x轴交于点A(﹣6,0)和点B(点A在点B左侧),与y轴交于点C,点P为线段AO上的一个动点,过点P作x轴的垂线l与抛物线交于点E,连接AE、EC.
(1)求抛物线的表达式及点C的坐标;
(2)连接AC交直线l于点D,则在点P运动过程中,当点D为EP中点时,S△ADP:S△CDE= ;
(3)如图2,当EC∥x轴时,点P停止运动,此时,在抛物线上是否存在点G,使得以点A、E、G为顶点的三角形是直角三角形?若存在,请求出点G的坐标,若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“今有善行者行一百步,不善行者行六十步”(出自《九章算术》)意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步,假定两者步长相等,据此回答以下问题:
(1)今不善行者先行一百步,善行者追之,不善行者再行六百步,问孰至于前,两者几何步隔之?即:走路慢的人先走100步,走路快的人开始追赶,当走路慢的人再走600步时,请问谁在前面,两人相隔多少步?
(2)今不善行者先行两百步,善行者追之,问几何步及之?即:走路慢的人先走200步,请问走路快的人走多少步才能追上走路慢的人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象经过点A(3,0),B(2,﹣3),并且以x=1为对称轴.
(1)求此函数的解析式;
(2)作出二次函数的大致图象;
(3)在对称轴x=1上是否存在一点P,使△PAB中PA=PB?若存在,求出P点的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设中学生体质健康综合评定成绩为x分,满分为100分,规定:85≤x≤100为A级,75≤x≤85为B级,60≤x≤75为C级,x<60为D级.现随机抽取福海中学部分学生的综合评定成绩,整理绘制成如下两幅不完整的统计图,请根据图中的信息,解答下列问题:
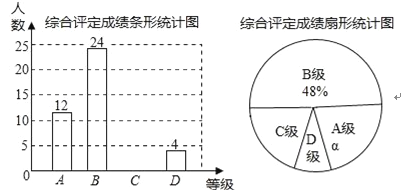
(1)在这次调查中,一共抽取了 名学生,α= %;
(2)补全条形统计图;
(3)扇形统计图中C级对应的圆心角为 度;
(4)若该校共有2000名学生,请你估计该校D级学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,在平面直角坐标系中,O为坐标原点,四边形OABC是矩形,点A.C的坐标分别为A(1O,0),C(0,4),点D是OA的中点,点P在BC边上运动。当△ODP是腰长为5的等腰三角形时,则点P的坐标是______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算:
(1)8+(-![]() )-5-(-0.25); (2)|-
)-5-(-0.25); (2)|-![]() |÷(
|÷(![]() -
-![]() )×(-4)2.
)×(-4)2.
(3)(![]() -
-![]() +
+![]() )×(-30); (4)(-1)3-(1-
)×(-30); (4)(-1)3-(1-![]() )÷3×[2-(-3)2].
)÷3×[2-(-3)2].
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com