
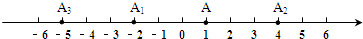
分析 序号为奇数的点在点A的左边,各点所表示的数依次减少3,序号为偶数的点在点A的右侧,各点所表示的数依次增加3,于是可得到A13表示的数为-17-3=-20,A12表示的数为16+3=19,则可判断点An与原点的距离不小于20时,n的最小值是13.
解答 解:第一次点A向左移动3个单位长度至点A1,则A1表示的数,1-3=-2;
第2次从点A1向右移动6个单位长度至点A2,则A2表示的数为-2+6=4;
第3次从点A2向左移动9个单位长度至点A3,则A3表示的数为4-9=-5;
第4次从点A3向右移动12个单位长度至点A4,则A4表示的数为-5+12=7;
第5次从点A4向左移动15个单位长度至点A5,则A5表示的数为7-15=-8;
…;
则A7表示的数为-8-3=-11,A9表示的数为-11-3=-14,A11表示的数为-14-3=-17,A13表示的数为-17-3=-20,
A6表示的数为7+3=10,A8表示的数为10+3=13,A10表示的数为13+3=16,A12表示的数为16+3=19,
所以点An与原点的距离不小于20,那么n的最小值是13.
故答案为:13.
点评 本题考查了规律型:认真观察、仔细思考,找出点表示的数的变化规律是解题关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
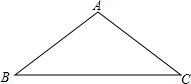 如图,在△ABC中,AB=AC=10,BC=16.
如图,在△ABC中,AB=AC=10,BC=16.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (a2)3=a5 | B. | 3$\sqrt{5}-\sqrt{5}$=3 | C. | $\root{3}{-27}$=-3 | D. | (a-b)2=a2-b2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
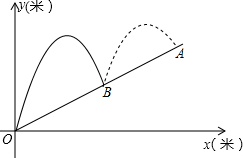 如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上)
如图,小张在山坡下点O向山上球洞A打高尔夫球,球的运行高度y(m)与运行的水平距离x(m)都满足y=-$\frac{1}{4}$(x+h)2+9(山坡看作一条直线),山坡上的各点的纵坐标与横坐标比是1:2,第一杆球落在B处(O、B、A在一条直线上) 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com