
��ͼ1����ƽ��ֱ������ϵ�У�����Rt��AOB��б��OB��x���ϣ�ֱ�� ��������Rt��AOB��ֱ�Ƕ���A����y����C�㣮
��������Rt��AOB��ֱ�Ƕ���A����y����C�㣮
(1) ���A���ꣻ
(2)����PΪx����һ���㣮��Q�������ǣ� ��
�� ������PAQ���Ե�AΪֱ�Ƕ���ĵ��������Σ����
������PAQ���Ե�AΪֱ�Ƕ���ĵ��������Σ���� ��ֵ��д����Q�����꣮
��ֵ��д����Q�����꣮
��3����(2)�������£���D������ƽ��������һ�㣬ʹ��A��P��Q��D�պ��ܹ���ƽ���ı��Σ���ֱ��д�����������ĵ�D������
��

��1��A��2��2������2��a=4��Q��4��1����3��D�����������1��1������5��3������3����2����
���������������1������A�ֱ���AM��y����M�㣬AN��x����N�㣬����ֱ�������ε����ʿ����A������Ϊ��a��a������Ϊ��A��ֱ��y=2x��2�ϣ�����A������������ʽ�������a��ֵ�������õ�A�����꣮
��2������AQ����A����AP��AQ��x����P�㣮��ASA��֤��AOP�ա�ABQ���ó���AOP=��ABQ=45���Ӷ����QB��OB������B�㡢Q�����������ȵó������
��3����Ϊ��D��A��P��Q���㹹��ƽ���ı��Σ��������������ۣ���ΪA��2��2����P����1��0����Q��4��1��������ƽ���ı��εĶԱ߷ֱ�ƽ������ȣ�
��QD��BA������������ĵ�D������ֱ���D1��5��3����D2��3����2������PD��QA������������ĵ�D������ֱ���D2��3����2����D3����1��1����
�����������1������A�ֱ���AM��y����M�㣬AN��x����N�㣬
�ߡ�AOB�ǵ���ֱ�������Σ�
��AM=AN��
���A��������a��a����
�ߵ�A��ֱ��y=2x��2�ϣ�
��a=2a��2��
���a=2��
��A��2��2��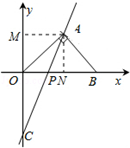
��2������AQ����A����AP��AQ��x����P�㣬
���APQΪ����ֱ�������Σ�
�ߡ�OAB=��PAQ=90��
���OAB����PAB=��PAQ����PAB��
���OAP=��BAQ��
�ڡ�APO���ABQ��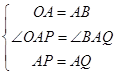
���APO�ա�ABQ��SAS����
���AOP=��ABO=45��
��QB��OB
��A��2��2��
��B��4��0��
��Q��������ǣ�a��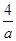 ����
����
��a=4��
��Q��4��1����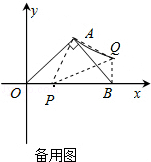
��3���ڣ�2���������£���D������ƽ��������һ�㣬ʹ��A��P��Q��D�պ��ܹ���ƽ���ı��Σ���D�������Ϊ����1��1������5��3������3����2����
���㣺һ�κ����ۺ��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�жԻ�վ�����˴��ģ�ĸĽ����Ľ���Ļ�վ��ԭ�е���ͨ��Ʊ�����⣬�������Զ���ӡ��Ʊ��������Ʊ���ڣ���ͼ,�߶� ��
�� �ֱ��ʾij�մ�����8�㵽����11�㣬ÿ����ͨ��Ʊ�����۳��ij�Ʊ��
�ֱ��ʾij�մ�����8�㵽����11�㣬ÿ����ͨ��Ʊ�����۳��ij�Ʊ�� ���ţ���ÿ��������Ʊ�����۳��ij�Ʊ��
���ţ���ÿ��������Ʊ�����۳��ij�Ʊ�� ���ţ�������Ʊʱ��
���ţ�������Ʊʱ�� ��Сʱ���ĺ���ͼ��
��Сʱ���ĺ���ͼ��
��1���� ���ţ���
���ţ��� ��Сʱ���ĺ�������ʽ��
��Сʱ���ĺ�������ʽ��
��2�������쿪��������Ʊ���ڸ�������ͨ��Ʊ���ڸ�����2����������8�㵽����11�㣬���ִ��ڹ��۳��ij�Ʊ��Ϊ2400�ţ����쿪��������Ʊ���ڵĸ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ˮ��ijУΪ�˿�չ����������������蹺��ijһƷ�Ƶ���ë�ס��������о���ÿֻ3Ԫ�ļ۸���ۣ�����һ���Թ�����һƷ����ë����100ֻ���û���ʵ���Żݣ��׳���ÿֻ��ë��ԭ�۵İ��۳��ۣ��ҳ�����15ֻ��ë���������ë��ÿֻ��ԭ�۵ľ��۳��ۣ�
��1��������ѡһ���У�һ���Թ���x��x��100��xΪ������ֻ��Ʒ����ë��д������Ǯy��Ԫ����x֮��ĺ�����ϵʽ��
��2����������260ֻ��Ʒ����ë�������ڼ׳����Լ׳��е��Żݷ�ʽ����һ���֣�ʣ�µ������ҳ������ҳ��е��Żݷ�ʽ������260ֻ��Ʒ����ë��������Ҫ������ԪǮ����ʱ�ڼס��������зֱ����Ʒ����ë�����ֻ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
ij�ľ��̵����۹�����ͬ��A��B����Ʒ�Ƶļ�����������2��AƷ�ƺ�3��BƷ�Ƶļ���������156Ԫ������3��AƷ�ƺ�1��BƷ�Ƶļ���������122Ԫ��
��1����������Ʒ�Ƽ������ĵ��ۣ�
��2��ѧУ��ѧǰϦ�����̵�������ּ�������չ�˴����������취���£�AƷ�Ƽ�������ԭ�۵İ������ۣ�BƷ�Ƽ�����5�����ϳ������ְ�ԭ�۵��������ۣ��蹺��x��AƷ�Ƶļ�������Ҫy1Ԫ������x��BƷ�Ƶļ�������Ҫy2Ԫ���ֱ����y1��y2����x�ĺ�����ϵʽ��
��3��С������ϵһ����ͬѧ���幺��ͬһƷ�Ƶļ����������������������������5������������Ʒ�Ƶļ����������㣿��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�ڹ���ij����������Ʊʱ���蹺����Ʊ��Ϊx���ţ����ܷ���Ϊy��Ԫ�����������ֹ�����
����һ������λ��������10000Ԫ����õ�λ������Ʊ�ļ۸�Ϊÿ��60Ԫ��
���ܷ��ã����������+��Ʊ�ѣ�
��������������Ʊ��ʽ��ͼ��ʾ��
����������⣺
��1������һ�У�y��x�ĺ�����ϵʽΪ ��
�������У���0��x��100ʱ��y��x�ĺ�����ϵʽΪ ��
��x��100ʱ��y��x�ĺ�����ϵʽΪ ��
��2�����������������Ʊ����100�ţ��㽫ѡ����һ�ַ�����ʹ�ܷ�����ʡ����˵�����ɣ�
��3���ס�������λ�ֱ���÷���һ��������������������Ʊ��700�ţ���ȥ�ܷ��ü�58000Ԫ����ס�������λ��������Ʊ�����ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ�˽�Լ��Դ����ѧָ��������ƾ�ס������С���ܲ��������һ��������Ʒ���������Է�����
| �˾�ס�����(ƽ����) | ����(��Ԫ/ƽ����) |
| ������30(ƽ����) | 0��3 |
| ����30ƽ���ײ�����m(ƽ����)����(45��m��60) | 0��5 |
| ����mƽ���ײ��� | 0��7 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�Ӽص��ҵأ�����һ��ƽ·��Ȼ����һ������·��С���ﳵ�Ӽس����������ҵغ�����ԭ·���ؼأ�;����Ϣ��һ��ʱ�䡣����С���ﳵ��ƽ·�����¡�����ʱ�ֱ𱣳�����ǰ��.��֪С���ﳵ���µ��ٶȱ�ƽ·�ϵ��ٶ�ÿСʱ��5km�����µ��ٶȱ���ƽ·�ϵ��ٶ�ÿСʱ��5km����С������xh�������y km�ĵط���ͼ�е�����OABCDE��ʾy��x֮��ĺ�����ϵ.
��1��С���ﳵ��ƽ·�ϵ��ٶ�Ϊ km/h����;����Ϣ�� h��
��2�����߶�AB��BC����ʾ��y�� ֮��ĺ�����ϵʽ��
֮��ĺ�����ϵʽ��
��3�����С�����ξ���;��ijһ�ص��ʱ����Ϊ0.15h����ô�õص���ض�Զ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
��ͼ�٣�����ABCD����ֱ������ϵ�У�����BC����x���ϣ�B��C����ߣ�����D����Ϊ��0,4����ֱ��MN�� ����x��ĸ�������ÿ��1����λ�ij���ƽ�ƣ�����ƽ�ƹ����и�ֱ�߱���ABCD�صõ��߶γ���Ϊm��ƽ��ʱ��Ϊt��m��t�ĺ���ͼ����ͼ����ʾ��
����x��ĸ�������ÿ��1����λ�ij���ƽ�ƣ�����ƽ�ƹ����и�ֱ�߱���ABCD�صõ��߶γ���Ϊm��ƽ��ʱ��Ϊt��m��t�ĺ���ͼ����ͼ����ʾ��
��1����գ���C������Ϊ ��
��ƽ�ƹ����У���ֱ���Ⱦ���B��D�е���һ�㣿 �����B����D����
��2����B������Ϊ ��n�� ��a�� ��
��3����ͼ�����߶�EF�Ľ���ʽ��
��4��tΪ��ֵʱ����ֱ��ƽ�֡�ABCD�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
Ϊ���������Լ��ˮ��ij�о����Ծ�����ˮ�շ�ʵ�С����ݼۡ�������ÿ����ˮ��������15��ʱ(����15��)�����û������շѣ���ÿ����ˮ������15��ʱ����������ÿ�ֲ����г����շѣ�С����4��5�·ݵ���ˮ�����շ�������±���
| �·� | ��ˮ��(��) | ˮ��(Ԫ) |
| 4 | 22 | 51 |
| 5 | 20 | 45 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com