
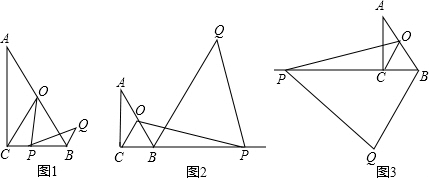
���� ��1�����ۣ�BQ=CP����ͼ1�У���PH��AB��CO��H���ɵá�PCH�ǵȱ������Σ�ֻҪ֤����POH�ա�QPB���ɣ�
��2��������PC=BQ����PH��AB��CO���ӳ�����H��֤���������ƣ�1����
��3����ͼ3�У���CE��OP��E����PE��ȡһ��F��ʹ��FP=FC������CF����CE=EO=a����FC=FP=2a��EF=$\sqrt{3}$a����Rt��PCE�У�PC=$\sqrt{P{E}^{2}+C{E}^{2}}$=$\sqrt{��2a+\sqrt{3}a��^{2}+{a}^{2}}$=��$\sqrt{6}$+$\sqrt{2}$��a������PC+CB=4���ɵ÷��̣�$\sqrt{6}$+$\sqrt{2}$��a+$\sqrt{2}$a=4�����a���ɽ�����⣻
��� �⣺��1�����ۣ�BQ=CP��
���ɣ���ͼ1�У���PH��AB��CO��H��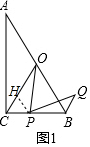
��Rt��ABC�У��ߡ�ACB=90�㣬��A=30�㣬��OΪAB�е㣬
��CO=AO=BO����CBO=60�㣬
���CBO�ǵȱ������Σ�
���CHP=��COB=60�㣬��CPH=��CBO=60�㣬
���CHP=��CPH=60�㣬
���CPH�ǵȱ������Σ�
��PC=PH=CH��
��OH=PB��
�ߡ�OPB=��OPQ+��QPB=��OCB+��COP��
�ߡ�OPQ=��OCP=60�㣬
���POH=��QPB����PO=PQ��
���POH�ա�QPB��
��PH=QB��
��PC=BQ��
��2��������PC=BQ��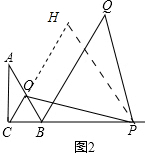
���ɣ���PH��AB��CO���ӳ�����H��
��Rt��ABC�У��ߡ�ACB=90�㣬��A=30�㣬��OΪAB�е㣬
��CO=AO=BO����CBO=60�㣬
���CBO�ǵȱ������Σ�
���CHP=��COB=60�㣬��CPH=��CBO=60�㣬
���CHP=��CPH=60�㣬
���CPH�ǵȱ������Σ�
��PC=PH=CH��
��OH=PB��
�ߡ�POH=60��+��CPO����QPO=60��+��CPQ��
���POH=��QPB����PO=PQ��
���POH�ա�QPB��
��PH=QB��
��PC=BQ��
��3����ͼ3�У���CE��OP��E����PE��ȡһ��F��ʹ��FP=FC������CF��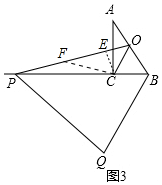
�ߡ�OPC=15�㣬��OCB=��OCP+��POC��
���POC=45�㣬
��CE=EO����CE=EO=a����FC=FP=2a��EF=$\sqrt{3}$a��
��Rt��PCE��PC=$\sqrt{P{E}^{2}+C{E}^{2}}$=$\sqrt{��2a+\sqrt{3}a��^{2}+{a}^{2}}$=��$\sqrt{6}$+$\sqrt{2}$��a��
��PC+CB=4��
�ࣨ$\sqrt{6}$+$\sqrt{2}$��a+$\sqrt{2}$a=4��
���a=4$\sqrt{2}$-2$\sqrt{6}$��
��PC=4$\sqrt{3}$-4��
�ɣ�2����֪BQ=PC��
��BQ=4$\sqrt{3}$-4��
���� ���⿼�鼸�α任�ۺ��⡢��ת�任���ȱ������ε��ж�������ȫ�������ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ�����ӳ��ø����ߣ�����ȫ�������ν�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
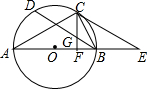 ��ͼ��ʾ���ԡ�ABC�ı�ABΪֱ������O����C�ڡ�O�ϣ�BD�ǡ�O���ң���A=��CBD������C��CF��AB�ڵ�F����BD�ڵ�G����C��CE��BD��AB���ӳ����ڵ�E��
��ͼ��ʾ���ԡ�ABC�ı�ABΪֱ������O����C�ڡ�O�ϣ�BD�ǡ�O���ң���A=��CBD������C��CF��AB�ڵ�F����BD�ڵ�G����C��CE��BD��AB���ӳ����ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
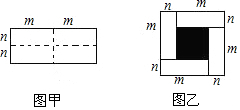 ��֪ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ȷֳ���С�鳤���Σ�Ȼ��ͼ�ҵ���״ƴ��һ�������Σ�
��֪ͼ����һ����Ϊ2m����Ϊ2n�ij����Σ���ͼ�������ü������ȷֳ���С�鳤���Σ�Ȼ��ͼ�ҵ���״ƴ��һ�������Σ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
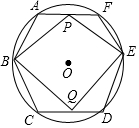 ��ͼ����O�뾶Ϊ4cm�����ڽ���������ABCDEF����P��Qͬʱ�ֱ��A��D�����������1cm/s�ٶ���AF��DC���յ�F��C�˶�������PB��QE��PE��BQ�����˶�ʱ��Ϊt��s����
��ͼ����O�뾶Ϊ4cm�����ڽ���������ABCDEF����P��Qͬʱ�ֱ��A��D�����������1cm/s�ٶ���AF��DC���յ�F��C�˶�������PB��QE��PE��BQ�����˶�ʱ��Ϊt��s�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com