
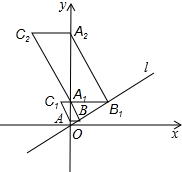
 ��ͼ����ƽ��ֱ������ϵ�У�ֱ��l����ԭ�㣬����y�����������е����Ϊ60�㣬����A��0��1����y��Ĵ���l�ڵ�B������B����ֱ��l�Ĵ��߽�y���ڵ�A1����A1B��ABΪ�ڱ���ƽ���ı���A1BAC1������A1��y��Ĵ��߽�ֱ��l�ڵ�B1������B1��ֱ��l�Ĵ��߽�y���ڵ�A2����A2B1��A1B1Ϊ�ڱ���ƽ���ı���A2B1A1C2��������C1������Ϊ��-$\sqrt{3}$��4������������������ȥ����Cn�������ǣ�-$\sqrt{3}$��4n-1��4n����
��ͼ����ƽ��ֱ������ϵ�У�ֱ��l����ԭ�㣬����y�����������е����Ϊ60�㣬����A��0��1����y��Ĵ���l�ڵ�B������B����ֱ��l�Ĵ��߽�y���ڵ�A1����A1B��ABΪ�ڱ���ƽ���ı���A1BAC1������A1��y��Ĵ��߽�ֱ��l�ڵ�B1������B1��ֱ��l�Ĵ��߽�y���ڵ�A2����A2B1��A1B1Ϊ�ڱ���ƽ���ı���A2B1A1C2��������C1������Ϊ��-$\sqrt{3}$��4������������������ȥ����Cn�������ǣ�-$\sqrt{3}$��4n-1��4n���� ���� �����ֱ��l�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x����B������Ϊ��x��1��������ֱ��l������B�����B������Ϊ��$\sqrt{3}$��1������Rt��A1AB���ó�AA1=3��OA1=4����ƽ���ı��ε����ʵó�A1C1=AB=$\sqrt{3}$����C1�������Ϊ��-$\sqrt{3}$��4��������-$\sqrt{3}$��40��41��������ֱ��l������B1�����B1������Ϊ��4$\sqrt{3}$��4������Rt��A2A1B1���ó�A1A2=12��OA2=16����ƽ���ı��ε����ʵó�A2C2=A1B1=4$\sqrt{3}$����C2�������Ϊ��-4$\sqrt{3}$��16��������-$\sqrt{3}$��41��42����ͬ�����ɵ�C3�������Ϊ��-16$\sqrt{3}$��64��������-$\sqrt{3}$��42��43���������ó����ɣ����Cn�������ǣ�-$\sqrt{3}$��4n-1��4n����
��� �⣺��ֱ��l����ԭ�㣬����y�����������е����Ϊ60�㣬
��ֱ��l�Ľ���ʽΪy=$\frac{\sqrt{3}}{3}$x��
��AB��y�ᣬ��A��0��1����
�����B��������x��1����
��B��x��1������y=$\frac{\sqrt{3}}{3}$x����1=$\frac{\sqrt{3}}{3}$x�����x=$\sqrt{3}$��
��B������Ϊ��$\sqrt{3}$��1����AB=$\sqrt{3}$����Rt��A1AB�У���AA1B=90��-60��=30�㣬��A1AB=90�㣬
��AA1=$\sqrt{3}$AB=3��OA1=OA+AA1=1+3=4��
��?ABA1C1��A1C1=AB=$\sqrt{3}$��
��C1���������-$\sqrt{3}$��4��������-$\sqrt{3}$��40��41����
��$\frac{\sqrt{3}}{3}$x=4�����x=4$\sqrt{3}$��
��B1��������4$\sqrt{3}$��4����A1B1=4$\sqrt{3}$��
��Rt��A2A1B1�У���A1A2B1=30�㣬��A2A1B1=90�㣬
��A1A2=$\sqrt{3}$A1B1=12��OA2=OA1+A1A2=4+12=16��
��?A1B1A2C2��A2C2=A1B1=4$\sqrt{3}$��
��C2���������-4$\sqrt{3}$��16��������-$\sqrt{3}$��41��42����
ͬ�����ɵ�C3�������Ϊ��-16$\sqrt{3}$��64��������-$\sqrt{3}$��42��43����
�Դ����ƣ���Cn�������ǣ�-$\sqrt{3}$��4n-1��4n����
�ʴ�Ϊ��-$\sqrt{3}$��41��42������-$\sqrt{3}$��4n-1��4n����
���� ���⿼����ƽ���ı��ε����ʣ���ֱ���������Լ�һ�κ������ۺ�Ӧ�ã��ȷֱ����C1��C2��C3������꣬�Ӷ����ֹ����ǽ���Ĺؼ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��-$\frac{3}{4}$ | B�� | x��-$\frac{3}{4}$ | C�� | x��$\frac{3}{4}$ | D�� | x��$\frac{3}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ��AD��BE�ֱ��ǡ�ABC�ĸߣ�AD=4��BC=6��AC=5����BE=$\frac{24}{5}$cm��
��ͼ��AD��BE�ֱ��ǡ�ABC�ĸߣ�AD=4��BC=6��AC=5����BE=$\frac{24}{5}$cm���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ABCΪ�ȱ������Σ���D��BC���ӳ����ϣ�CEƽ�֡�ACD���ҡ�ADE=60�㣮
��ͼ����ABCΪ�ȱ������Σ���D��BC���ӳ����ϣ�CEƽ�֡�ACD���ҡ�ADE=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2��1��2 | B�� | 2��3��4 | C�� | 1��1��$\sqrt{2}$ | D�� | 4��5��6 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com