
【题目】如图,直线AB,CD相交于点O,OE⊥AB,垂足为O,OF平分∠AOE,∠1=15°,则下列结论中不正确的是( )
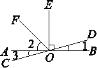
A. ∠2=45° B. ∠1=∠3 C. ∠EOD与∠3互为余角 D. ∠FOD=110°
【答案】D
【解析】根据垂直的定义可得∠AOE=90°,再根据角平分线的定义求出∠2=45°,根据对顶角相等可得∠1=∠3,根据互余的定义求出∠EOD与∠3互为余角,根据平角等于180°列式计算即可求出∠FOD=120°.
A、∵OE⊥AB,
∴∠AOE=90°,
∵OF平分∠AOE,
∴∠2=![]() ∠AOE=
∠AOE=![]() ×90°=45°,故本选项错误;
×90°=45°,故本选项错误;
B、∵∠1、∠3是对顶角,
∴∠1=∠3,故本选项错误;
C、∵∠EOD+∠1=∠BOE=90°,
∴∠EOD+∠3=90°,
∴∠EOD与∠3互为余角,故本选项错误;
D、∠FOD=180°-∠1-∠2=180°-15°-45°=120°,故本选项正确.
故选:D.


科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,﹣3)三点,直线l是抛物线的对称轴.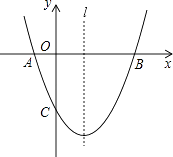
(1)求抛物线的函数关系式;
(2)设点P是直线l上的一个动点,当点P到点A、点B的距离之和最短时,求点P的坐标;
(3)点M也是直线l上的动点,且△MAC为等腰三角形,请直接写出所有符合条件的点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,下列能判定AB∥CD的条件有( )个.
(1)∠B+∠BCD=180°;(2)∠1=∠2;(3)∠3=∠4;(4)∠B=∠5.

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果,
投篮次数(n) | 50 | 100 | 150 | 209 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 175 |
投中频率(n/m) | 0.56 | 0.60 |
| 0.49 |
|
|
(1)计算并填写表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如果-axym是关于x,y的单项式,且系数是4,次数是5,那么a与m的值分别是________;
(2)如果-(a-2)xym是关于x,y的五次单项式,那么a与m应满足的条件是____________;
(3)如果单项式2x3y4与-![]() x2zn的次数相同,那么n=________.
x2zn的次数相同,那么n=________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=BC=8,AO=BO,点M是射线CO上的一个动点,∠AOC=60°,则当△ABM为直角三角形时,AM的长为____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
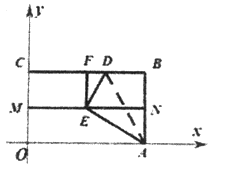
【题目】定义:把函数y=bx+a和函数y=ax+b(其中a,b是常数,且a≠0,b≠0)称为一对交换函数,其中一个函数是另一个函数的交换函数.比如,函数y=4x+1是函数y=x+4的交换函数,等等.
(1)直接写出函数y=2x+1的交换函数;_________________;并直接写出这对交换函数和x轴所围图形的面积为_____________________________;
(2)若一次函数y=ax+2a和其交换函数与x轴所围图形的面积为3,求a的值.
(3)如图,在平面直角坐标xOy中,矩形OABC中,点C(0, ![]() ),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数
),M、N分别是线段OC、AB的中点,将△ABD沿着折痕AD翻折,使点B的落点E恰好落在线段MN的中点,点F是线段BC的中点,连接EF,若一次函数![]() 和
和![]() 与线段EF始终都有交点,则m的取值范围为_____________________.
与线段EF始终都有交点,则m的取值范围为_____________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com