【题目】正方形
的边长为4,
为正方形内任意一点，连接
、
、
,
的最小值为____________.
【答案】
【解析】
顺时针旋转△APD，可得△PAP为等边三角形，即得PA+PB+PD=PB+PP+PD，所以只要点B、P、P、D在同一条直线上时，PB+PP+PD值最小，最小值为线段BD长，根据勾股定理求线段BD长.
解：如图，以A为中心，逆时针旋转△APD至△APD，则△PAP为等边三角形，则PA+PB+PD=PB+PP+PD，
∴当点B、P、P、D在同一条直线上时，PB+PP+PD值最小，最小值为线段BD长.
作直线DM⊥AB交BA延长线于M点，
∵AD=AD=4，∠DAM=30°，
∴DM=2，
∴根据勾股定理得，AM=
，
∴BM=4+，
∴根据勾股定理得，
BD=
=
= .
∴
的最小值为.
故答案为：
科目：初中数学 来源： 题型：
【题目】如图，已知二次函数
（
）的图象与x轴交于点A（﹣1，0），对称轴为直线x=1，与y轴的交点B在（0，2）和（0，3）之间（包括这两点），下列结论：
①当x＞3时，y＜0；
②3a+b＜0；
③
；
④
；
其中正确的结论是（ ）
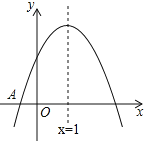
A.①③④B.①②③C.①②④D.①②③④
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】元旦放假期间，小明和小华准备到西安的大雁塔（记为A）、白鹿原（记为B）、兴庆公园（记为C）、秦岭国家植物园（记为D）中的一个景点去游玩，他们各自在这四个景点中任选一个，每个景点被选中的可能性相同．
（1）求小明选择去白鹿原游玩的概率；
（2）用树状图或列表的方法求小明和小华都选择去秦岭国家植物园游玩的概率．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】教材呈现：下图是华师版九年级上册数学教材第77页的部分内容.
猜想：
如图，在
中，点
分别是
与
的中点，根据画出的图形，可以猜想：
，且
.
对此，我们可以用演绎推理给出证明.
证明：在中，
∵点分别是与的中点，
∴
.
请根据教材提示，结合图①，写出完整的证明过程.
结论应用：
如图②在四边形
中，
，点
是对角线
的中点，
是
中点，
是中点，
与相交于点
.
（1）求证：
；
（2）若
，
，
，则
_______________.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读下面材料，完成（1）～（3）题．
数学课上，老师出示了这样一道题：
如图1，△ABC中，AC＝BC＝a，∠ACB＝90°，点D在AB上，且AD＝kAB（其中0＜k＜
），直线CD绕点D顺时针旋转90°与直线CB绕点B逆时针旋转90°后相交于点E，探究线段DC、DE的数量关系，并证明．
同学们经过思考后，交流了自己的想法：
小明：“通过观察和度量，发现DC与DE相等”；
小伟：“通过构造全等三角形，经过进一步推理，可以得到DC与DE相等”
小强：“通过进一步的推理计算，可以得到BE与BC的数量关系”
老师：“保留原题条件，连接CE交AB于点O．如果给出BO与DO的数量关系，那么可以求出COEO的值”
（1）在图1中将图补充完整，并证明DC＝DE；
（2）直接写出线段BE与BC的数量关系 （用含k的代数式表示）；
（3）在图2中将图补充完整，若BO＝
DO，求COEO的值（用含a的代数式表示）．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】有4张不透明的卡片,除正面上的图案不同外,其他均相同,将这4张卡片背面向上洗匀后放在桌面上.
(1)从中随机油取1张卡片,卡片上的图案是中心对称图形的概率为_________;
(2)若从中随机抽取1张卡片后不放回,再随机抽取1张,请用列表的方法,求两次所抽取的卡片恰好都是中心对称图形的概率.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，AB=AC=5，BC=4
,D为边AB上一动点(B点除外)，以CD为一边作正方形CDEF，连接BE，则△BDE面积的最大值为______.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】暑假快到了，父母找算带兄妹俩去某个景点旅游一次，长长见识，可哥哥坚持去黄山，妹妹坚持去泰山，争执不下，父母为了公平起见，决定设计一款游戏，若哥哥赢了就去黄山，妹妹赢了就去泰山．下列游戏中，不能选用的是（ ）
A. 掷一枚硬币，正面向上哥哥赢，反面向上妹妹赢
B. 同时掷两枚硬币，两枚都正面向上，哥哥赢，一正一反向上妹妹赢
C. 掷一枚骰子，向上的一面是奇数则哥哥赢，反之妹妹赢
D. 在不透明的袋子中装有两黑两红四个球，除颜色外，其余均相同，随机摸出一个是黑球则哥哥赢，是红球则妹妹赢
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
