练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图是某居民小区的一块长为b米，宽为2a米的长方形空地，为了美化环境，准备在这个长方形的四个顶点处各修建一个半径为a米的扇形花台，然后在花台内种花，其余部分种草．如果建造花台及种花费用每平方米需要资金100元，种草每平方米需要资金50元，那么美化这块空地共需资金多少元？

    【答案】(50πa2＋100ab)元.

    【解析】花台面积为πa2平方米，所需资金为πa2×100．草地面积为（2ab-πa2）平方米，所需资金为（2ab-πa2）×50．共需资金为花台所需资金+草地所需资金．

    花台面积为πa2平方米，草地面积为(2ab－πa2)平方米，所需资金为100×πa2＋50(2ab－πa2)＝(50πa2＋100ab)元．

    即美化这块空地共需资金(50πa2＋100ab)元．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

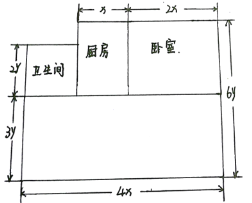
    【题目】如图是一套房子的平面图,尺寸如图.

    (1)这套房子的总面积是多少?(用含x、y的代数式表示)

    (2)如果x=1.8米,y=1米,那么房子的面积是多少平方米?如果每平方米房价为5万元,那么房屋总价多少万元?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A、B两地在数轴上相距20米，A地在数轴上表示的点为-8，小乌龟从A地出发沿数轴往B地方向前进，第一次前进1米，第二次后退2米，第三次再前进3米，第四次又后退4米，……，按此规律行进，（数轴的一个单位长度等于1米）

    （1）求B地在数轴上表示的数；

    （2）若B地在原点的左侧，经过第五次行进后小乌龟到达点P，第六次行进后到达点Q，则点P和点Q到点A的距离相等吗？请说明理由；

    （3）若B地在原点的右侧，那么经过30次行进后，小乌龟到达的点与点B之间的距离是多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在直角坐标系中，四边形OABC为矩形，A（6，0），C（0，3），点M在边OA上，且M（4，0），P、Q两点同时从点M出发，点P沿x轴向右运动；点Q沿x轴先向左运动至原点O后，再向右运动到点M停止，点P随之停止运动．P、Q两点运动的速度分别为每秒1个单位、每秒2个单位．以PQ为一边向上作正方形PRLQ．设点P的运动时间为t（秒），正方形PRLQ与矩形OABC重叠部分（阴影部分）的面积为S（平方单位）．

    （1）用含t的代数式表示点P的坐标．

    （2）分别求当t=1，t=3时，线段PQ的长．

    （3）求S与t之间的函数关系式．

    （4）直接写出L落在第一象限的角平分线上时t的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

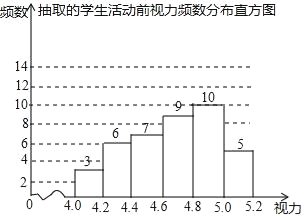
    【题目】为了保护视力，学校开展了全校性的视力保健活动，活动前，随机抽取部分学生，检查他们的视力，结果如图所示（数据包括左端点不包括右端点，精确到0.1）；活动后，再次检查这部分学生的视力，结果如表所示

    分组

    频数

    4.0≤x＜4.2

    2

    4.2≤x＜4.4

    3

    4.4≤x＜4.6

    5

    4.6≤x＜4.8

    8

    4.8≤x＜5.0

    17

    5.0≤x＜5.2

    5

    （1）求活动所抽取的学生人数；

    （2）若视力达到4.8及以上为达标，计算活动前该校学生的视力达标率；

    （3）请选择适当的统计量，从两个不同的角度评价视力保健活动的效果．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）图（1）是一个长为2m，宽为2n的矩形，把此矩形沿图中虚线用剪刀均分为四个小长方形，然后按图（2）的形状拼成一个大正方形．请问：这两个图形的什么量不变？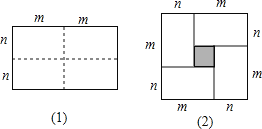

    （2）把所得的大正方形面积比原矩形的面积多出的阴影部分的面积用含m，n的代数式表示为（m-n）2或m2-2mn+n2 ．
    （3）由前面的探索可得出的结论是：在周长一定的矩形中，当 时，面积最大．
    （4）若矩形的周长为24cm，则当边长为多少时，该图形的面积最大？最大面积是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形ABCD的边BC绕点C逆时针旋转90°到CE，连接AC、DE、BE，AC与DE相交于F，则∠AFD＝_____．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】阅读理解下面内容，并解决问题：

    善于思考的小明在学习《实数》一章后，自己探究出了下面的两个结论：

    ①，，和都是9×4的算术平方根，

    而9×4的算术平方根只有一个，所以=．

    ②，，和都是9×16的算术平方根，

    而9×16的算术平方根只有一个，所以　　．

    请解决以下问题：

    （1）请仿照①帮助小明完成②的填空，并猜想：一般地，当a≥0，b≥0时，与、之间的大小关系是怎样的？

    （2）再举一个例子，检验你猜想的结果是否正确．

    （3）运用以上结论，计算：的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在我国南宋数学家杨辉（约13世纪）所著的《详解九章算术》（1261年）一书中，用下图的三角形解释二项和的乘方规律．杨辉在注释中提到，在他之前北宋数学家贾宪（1050年左右）也用过上述方法，因此我们称这个三角形为“杨辉三角”或“贾宪三角”．杨辉三角两腰上的数都是，其余每一个数为它上方（左右）两数的和．事实上，这个三角形给出了的展开式（按的次数由大到小的顺序）的系数规律．例如，此三角形中第三行的个数，恰好对应着展开式中的各项系数，第四行的个数，恰好对应着展开式中的各项系数，等等．请依据上面介绍的数学知识，解决下列问题：

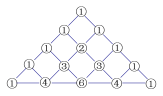
    （1）写出的展开式；

    （2）利用整式的乘法验证你的结论．

    查看答案和解析>>

    同步练习册答案