
【题目】小李的活鱼批发店以44元/公斤的价格从港口买进一批2000公斤的某品种活鱼,在运输过程中,有部分鱼未能存活,小李对运到的鱼进行随机抽查,结果如表一.由于市场调节,该品种活鱼的售价与日销售量之间有一定的变化规律,表二是近一段时间该批发店的销售记录.
(1)请估计运到的2000公斤鱼中活鱼的总重量;(直接写出答案)
(2)按此市场调节的观律,
①若该品种活鱼的售价定为52.5元/公斤,请估计日销售量,并说明理由;
②考虑到该批发店的储存条件,小李打算8天内卖完这批鱼(只卖活鱼),且售价保持不变,求该批发店每日卖鱼可能达到的最大利润,并说明理由.


【答案】(1) 估计运到的2000公斤鱼中活鱼的总重量为1760公斤;(2) ①可以估计当活鱼的售价定为52.5元/公斤时,日销售量为300公斤;②售价定为54.5元/公斤,每日卖鱼可能达到的最大利润为990元.
【解析】
(1)用总质量乘以0.880可得;
(2)①由表知,售价每增加1元,日销售量就减少40公斤,据此求解可得;
②由售价每增加x元/公斤,可估计日销售量在400公斤的基础上减少40x公斤,设批发店每日卖鱼的利润为w,根据总利润=每公斤的利润×销售量列出函数解析式,在根据题意求出增加的单价的取值范围,利用二次函数的性质求解可得.
(1) 估计运到的2000公斤鱼中活鱼的总重量为1760公斤;
(2) ①根据表二的销售记录可知,活鱼的售价每增加1元,其日销售量就减少40公斤,所以按此变化规律可以估计当活鱼的售价定为52.5元/公斤时,日销售量为300公斤;
②由(2) ①,若活鱼售价在50元/公斤的基础上,售价增加![]() 元/公斤,则可估计日销售量在400公斤的基础上减少40
元/公斤,则可估计日销售量在400公斤的基础上减少40![]() 公斤,
公斤,
设批发店每日卖鱼的最大利润为![]() ,
,
由题得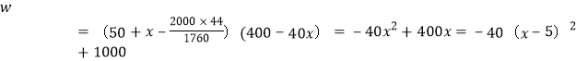
由“在8天内卖完这批活鱼”,可得![]() ,解得
,解得![]() .根据实际意义,有
.根据实际意义,有![]() ;解得
;解得![]() .
.
所以![]()
因为![]() ,
,
所以当![]() 时,
时,![]() 的增大而增大,
的增大而增大,
所以售价定为54.5元/公斤,每日卖鱼可能达到的最大利润为990元.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣5,1),B(﹣2,2),C(﹣1,4),请按下列要求画图:
(1)将△ABC先向右平移4个单位长度、再向下平移1个单位长度,得到△A1B1C1,画出△A1B1C1;
(2)画出与△ABC关于原点O成中心对称的△A2B2C2,并直接写出点A2的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,AB=AC,∠BAC=α,直线l经过点A(不经过点B或点C),点C关于直线l的对称点为点D,连接BD,CD.
(1)如图1,
①求证:点![]() 在以点
在以点![]() 为圆心,
为圆心,![]() 为半径的圆上.
为半径的圆上.
②直接写出∠BDC的度数(用含α的式子表示)为___________.
(2)如图2,当α=60°时,过点D作BD的垂线与直线l交于点E,求证:AE=BD;
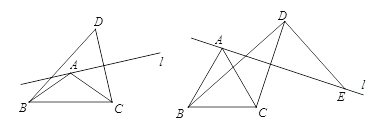
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们把三边长的比为3:4:5的三角形称为完全三角形,记命题A:“完全三角形是直角三角形”.若命题B是命题A的逆命题,请写出命题B:______________________;并写出一个例子(该例子能判断命题B是错误的)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子中,装有3个分别写有数字6,﹣2,7的小球,他们的形状、大小、质地完全相同,搅拌均匀后,先从盒子里随机抽取1个小球,记下小球上的数字后放回盒子,搅拌均匀后再随机取出1个小球,再记下小球上的数字.
(1)用列表法或树状图法(树状图也称树形图)中的一种方法,写出所有可能出现的结果;
(2)求两次取出的小球上的数字相同的概率P.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(﹣![]() ,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
,0),点B(0,1)把△ABO绕点O顺时针旋转,得△A'B'O,点A,B旋转后的对应点为A',B',记旋转角为α(0°<α<360°).
(1)如图①,当点A′,B,B′共线时,求AA′的长.
(2)如图②,当α=90°,求直线AB与A′B′的交点C的坐标;
(3)当点A′在直线AB上时,求BB′与OA′的交点D的坐标(直接写出结果即可)
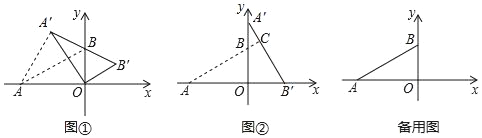
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(k﹣5)x+1﹣k=0(其中k为常数).
(1)求证无论k为何值,方程总有两个不相等实数根;
(2)已知函数y=x2+(k﹣5)x+1﹣k的图象不经过第三象限,求k的取值范围;
(3)若原方程的一个根大于3,另一个根小于3,求k的最大整数值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com