
【题目】如图,已知AC⊥BC,垂足为C,AC=4,BC=3 ![]() ,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB.
,将线段AC绕点A按逆时针方向旋转60°,得到线段AD,连接DC,DB. 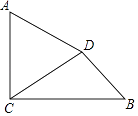
(1)线段DC=;
(2)求线段DB的长度.
【答案】
(1)4
(2)解:作DE⊥BC于点E.
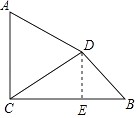
∵△ACD是等边三角形,
∴∠ACD=60°,
又∵AC⊥BC,
∴∠DCE=∠ACB﹣∠ACD=90°﹣60°=30°,
∴Rt△CDE中,DE= ![]() DC=2,
DC=2,
CE=DCcos30°=4× ![]() =2
=2 ![]() ,
,
∴BE=BC﹣CE=3 ![]() ﹣2
﹣2 ![]() =
= ![]() .
.
∴Rt△BDE中,BD= ![]() =
= ![]() =
= ![]()
【解析】解:(1)∵AC=AD,∠CAD=60°,
∴△ACD是等边三角形,
∴DC=AC=4.
故答案是:4;
【考点精析】解答此题的关键在于理解旋转的性质的相关知识,掌握①旋转后对应的线段长短不变,旋转角度大小不变;②旋转后对应的点到旋转到旋转中心的距离不变;③旋转后物体或图形不变,只是位置变了.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=12,以BC为斜边在矩形外部作直角三角形BEC,F为CD的中点,则EF的最大值为( ) 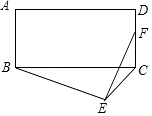
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
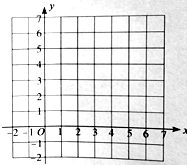
【题目】如图所示网格是由边长为1的小正方形组成,点A,B,C位置如图所示,在网格中确定点D,使以A,B,C,D为顶点的四边形的所有内角都相等. 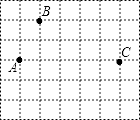
(1)确定点D的位置并画出以A,B,C,D为顶点的四边形;
(2)直接写出(1)中所画出的四边形的周长和面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
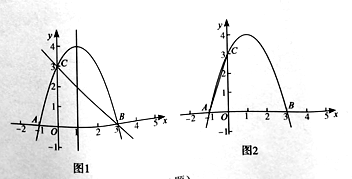
【题目】 抛物线![]() 与
与![]() 轴交于点
轴交于点![]() (
(![]() 在
在![]() 的左侧),与
的左侧),与![]() 轴交于点
轴交于点![]() .
.
⑴求直线![]() 的解析式;
的解析式;
⑵抛物线的对称轴上存在点![]() ,使
,使![]() ,利用图
,利用图![]() 求点
求点![]() 的坐标;
的坐标;
⑶点![]() 在
在![]() 轴右侧的抛物线上,利用图
轴右侧的抛物线上,利用图![]() 比较
比较![]() 与
与![]() 的大小,并说明理由.
的大小,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线![]() 的解析式为
的解析式为![]() ,分别交
,分别交![]() 轴、
轴、![]() 轴于点
轴于点![]() .
.
⑴写出![]() 两点的坐标,并画出直线
两点的坐标,并画出直线![]() 的图象;
的图象;
⑵将直线![]() 向上平移
向上平移![]() 个单位得到
个单位得到![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() .作出
.作出![]() 的图象,
的图象,![]() 的解析式是 .
的解析式是 .
⑶将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,
,![]() 交
交![]() 于点
于点![]() .作出
.作出![]() 的图象,
的图象,![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示为某汽车行驶的路程S(km)与时间t(min)的函数关系图,观察图中所提供的信息解答下列问题: 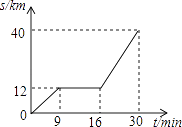
(1)汽车在前9分钟内的平均速度是多少?
(2)汽车中途停了多长时间?
(3)当16≤t≤30时,求S与t的函数关系式?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com