
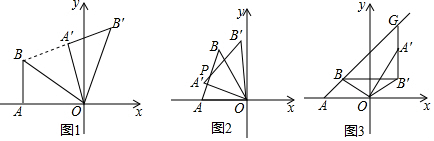
分析 (1)首先证明∠ABA′+∠AOA′=180°,由OB=OB′,再证明∠OBB′=∠B′=∠ABO,可得2∠ABO+θ=180°,由此即可解决问题.
(2)结论:OP平分∠APB′;如图2中,连接OP,作OE⊥A′B′于E,OF⊥AB于F.只要证明OE=OF即可解决问题.
(3)如图3中,作B′M⊥x轴于M,延长MB′到A″所得B′A″=5,连接OA″,作BN⊥OA于N.利用重合法证明A′与A″重合,求出直线AB的解析式即可求出点G的坐标.
解答 解:(1)如图1中,
∵△OA′B′是由△OAB旋转所得,
∴∠OA′B′=∠OAB,∠ABO=∠B′,
∵B′、A′、B三点共线,
∴∠BA′O+∠OA′B′=180°,
∴∠OAB+∠OA′B=180°,
∴∠ABA′+∠AOA′=180°,
∵OB=OB′,
∴∠OBB′=∠B′=∠ABO,
∴2∠ABO+θ=180°,
∴∠ABO=90°-$\frac{1}{2}$θ;
故答案为90°-$\frac{1}{2}$θ.
(2)结论:OP平分∠APB′.理由如下:
如图2中,连接OP,作OE⊥A′B′于E,OF⊥AB于F.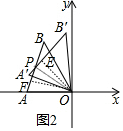
∵△OAB≌△OA′B′,
∴OE=OF,
∴∠OPE=∠OPF,
∴OP平分∠APB′;
(3)如图3中,作B′M⊥x轴于M,延长MB′到A″所得B′A″=5,连接OA″,作BN⊥OA于N.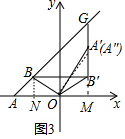
∵A(-10,0),B(-6,3),BB′∥AM,OB=OB′,
∴OA=10,NB=3,AN=4,B′(6,3),
∴OM=6,BM′=3,
在Rt△ABN中,∵AN=6,BN=3,
∴AB=$\sqrt{{3}^{2}+{4}^{2}}$=5,
在Rt△OA″M中,∵OM=6,MA″=8,
∴OA″=$\sqrt{{6}^{2}+{8}^{2}}$=10,
∴OA=OB′,B′A″=AB,OA″=OA,
∴△OB′A″≌△OBA,
∴A′与A″重合,
∴A′B′⊥OM,
∵直线AB的解析式为y=$\frac{3}{4}$x+$\frac{15}{2}$,
∴G(6,12).
点评 本题考查三角形综合题、旋转变换、全等三角形的判断和性质、四边形内角和定理、一次函数的应用、勾股定理、角平分线的判定定理等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,学会利用重合法解决有关问题,属于中考压轴题.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案 优翼小帮手同步口算系列答案
优翼小帮手同步口算系列答案科目:初中数学 来源: 题型:解答题
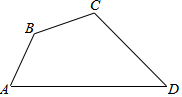 四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.
四边形ABCD中,AB=$\sqrt{6}$,BC=5-$\sqrt{3}$,CD=6,∠ABC=135°,∠BCD=120°,求AD的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.
小军同学拿着边长为acm的等边三角形硬纸片从图示的位置开始在数轴上顺时针无滑动地向右滚动,当三角形的一个顶点落在x=b处时,停止滚动,且(a-1)2+|b-5|=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).
如图,△ABC三个顶点的坐标分别为A(-1,3),B(-4,1),C(-2,1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com