
 ,
, =90°.
=90°.
|


 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案科目:初中数学 来源:不详 题型:解答题
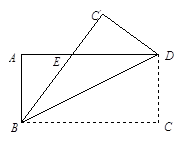
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
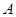 →
→ →
→ →
→ 的小路(
的小路( 、
、 分别是
分别是 、
、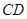 中点).极少数同学为了走“捷径”,沿线段
中点).极少数同学为了走“捷径”,沿线段 行走,破坏了草坪,实际上他们仅少走了________米。
行走,破坏了草坪,实际上他们仅少走了________米。
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com