
【题目】直角△ABC中,∠C=90°,点D,E分别是边AC,BC上的点,点P是一动点.令∠PDA=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若点P在线段AB上,如图①,且∠α=50°,则∠1+∠2= ;
(2)若点P在斜边AB上运动,如图②,则∠α、∠1、∠2之间的关系为 ;
(3)如图③,若点P在斜边BA的延长线上运动(CE<CD),请直接写出∠α、∠1、∠2之间的关系: ;
(4)若点P运动到△ABC形外(只需研究图④情形),则∠α、∠1、∠2之间有何关系?并说明理由.

【答案】(1)140°(2)∠1+∠2=90°+∠α(3)∠2﹣∠1=90°+∠α;∠2=∠1+90°;∠1﹣∠2=∠α﹣90°(4)∠2=90°+∠1﹣α,理由见解析
【解析】试题分析:(1)连接PC,根据三角形的一个外角等于与它不相邻的两个内角的和可得∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,再表示出∠1+∠2即可;
(2)利用(1)中所求得出答案即可;
(3)利用三角外角的性质分三种情况讨论即可;
(4)利用三角形内角和定理以及邻补角的性质可得出.
解:(1)如图,连接PC,
∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠DPE=∠α=50°,∠C=90°,
∴∠1+∠2=50°+90°=140°,
故答案为:140°;

(2)连接PC,
∵∠1=∠PCD+∠CPD,∠2=∠PCE+∠CPE,
∴∠1+∠2=∠PCD+∠CPD+∠PCE+∠CPE=∠DPE+∠C,
∵∠C=90°,∠DPE=∠α,
∴∠1+∠2=90°+∠α;
故答案为:∠1+∠2=90°+∠α;

(3)如图1,
∵∠2=∠C+∠1+∠α,
∴∠2﹣∠1=90°+∠α;
如图2,∠α=0°,∠2=∠1+90°;
如图3,∵∠2=∠1﹣∠α+∠C,
∴∠1﹣∠2=∠α﹣90°.

故答案为;∠2﹣∠1=90°+∠α;∠2=∠1+90°;∠1﹣∠2=∠α﹣90°.
(4)

∵∠PFD=∠EFC,
∴180°﹣∠PFD=180°﹣∠EFC,
∴∠α+180°﹣∠1=∠C+180°﹣∠2,
∴∠2=90°+∠1﹣α.
故答案为:∠2=90°+∠1﹣α.


 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:初中数学 来源: 题型:
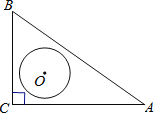
【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1 B.1≤r≤![]() C.1≤r≤
C.1≤r≤![]() D.1≤r≤4
D.1≤r≤4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小马虎同学在计算某个多边形的内角和时得到1840°,老师说他算错了,于是小马虎认真地检查了一遍发现漏算了一个内角,求漏算的那个内角是多少度?这个多边形是几边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,∠ACB=90°,D是AB的中点,点E是AB边上一点.
(1)BF⊥CE于点F,交CD于点G(如图①).求证:AE=CG;
(2)AH⊥CE,垂足为H,交CD的延长线于点M(如图②),找出图中与BE相等的线段,并证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙P在第一象限,半径为3,动点A沿着⊙P运动一周,在点A运动的同时,作点A关于原点O的对称点B,再以AB为底边作等腰三角形△ABC,点C在第二象限,且sinA=0.8,点C随点A运动所形成的图形的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AB为直径的⊙O分别与BC,AC交于点D,E,过点D作⊙O的切线DF,交AC于点F.
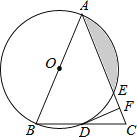
(1)求证:DF⊥AC;
(2)若⊙O的半径为4,∠CDF=22.5°,求阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=BC,斜边AB=2,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,弧EF经过点C,则图中阴影部分的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
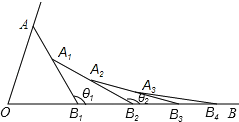
【题目】如图所示,已知∠AOB=α,在射线OA、OB上分别取点OA1=OB1,连结A1B1,在B1A1、B1B上分别取点A2、B2,使B1B2=B1A2,连结A2B2…按此规律下去,记∠A2B1 B2=θ1,∠A3B2B3=θ2,…,∠An+1Bn Bn+1=θn,则θ2016﹣θ2015的值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com