
【题目】某商场计划购进一批自行车. 男式自行车价格为![]() 元/辆,女式自行车价格为
元/辆,女式自行车价格为![]() 元/辆,要求男式自行车比女式单车多
元/辆,要求男式自行车比女式单车多![]() 辆,设购进女式自行车
辆,设购进女式自行车![]() 辆,购置总费用为
辆,购置总费用为![]() 元.
元.
(1)求购置总费用![]() (元)与女式单车
(元)与女式单车![]() (辆)之间的函数关系式;
(辆)之间的函数关系式;
(2)若两种自行车至少需要购置![]() 辆,且购置两种自行车的费用不超过
辆,且购置两种自行车的费用不超过![]() 元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
元,该商场有几种购置方案?怎样购置才能使所需总费用最低,最低费用是多少?
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
【题目】我们给出如下定义:顺次连接任意一个四边形各边中点所得的四边形叫中点四边形.

(1)如图1,四边形ABCD中,点E,F,G,H分别为边AB,BC,CD,DA的中点.求证:中点四边形EFGH是平行四边形;
(2)如图2,点P是四边形ABCD内一点,且满足PA=PB,PC=PD,∠APB=∠CPD,点E,F,G,H分别为边AB,BC,CD,DA的中点,猜想中点四边形EFGH的形状,并证明你的猜想;
(3)若改变(2)中的条件,使∠APB=∠CPD=90°,其他条件不变,直接写出中点四边形EFGH的形状.(不必证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知菱形ABCD,对角线交点为O,延长CD至E且CD=DE.下列判断正确个数是( )
(1)∠AOB=90°;(2)AE=2OD;(3)∠OAE=90°;(4)∠AEO=∠CEO.
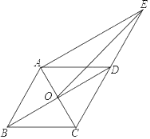
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】旺财水果店每天都会进一些草莓销售,在一周销售过程中他发现每天的销售量y(单位:千克)会随售价x(单位:元/千克)而变化,部分数据记录如表
售价x(单位:元/千克) | 30 | 25 | 20 |
每天销售量y(单位:千克) | 5 | 55 | 105 |
如果已知草莓每天销量y与售价x(30.5>x>14)满足一次函数关系.
(1)请根据表格中数据求出这个一次函数关系式;
(2)如果进价为14元/千克,请判断售价分别定为20元/千克和25元/千克,哪天的销售利润更高?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,AB是⊙O的直径,BD=OB,∠CAB=30°,请根据已知条件和图形,写出三个正确的结论(AO=BO=BD除外)________;_____________;____________.
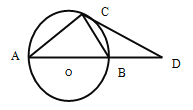
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题背景】
如图①所示,在正方形ABCD的内部,作∠DAE=∠ABF=∠BCG=∠CDH,根据三角形全等的条件,易得△DAE≌△ABF≌△BCG≌△CDH,从而得到四边形EFGH是正方形.
【类比研究】
如图②所示,在正△ABC的内部,作∠BAD=∠CBE=∠ACF,AD,BE,CF两两相交于D,E,F三点(D,E,F三点不重合).
(1)△ABD,△BCE,△CAF是否全等?如果是,请选择其中一对进行证明;
(2)△DEF是否为正三角形?请说明理由;
(3)连结AE,若AF=DF,AB=7,求△DEF的边长.
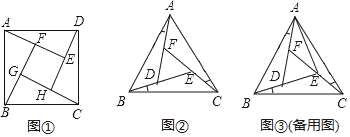
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,直线y=![]() x与双曲线
x与双曲线![]() 交于A、B两点,且点A的坐标为(6,m).
交于A、B两点,且点A的坐标为(6,m).
(1)求双曲线![]() 的解析式;
的解析式;
(2)点C(n,4)在双曲线![]() 上,求△AOC的面积;
上,求△AOC的面积;
(3)在(2)的条件下,在x轴上找出一点P,使△AOC的面积等于△AOP的面积的三倍.请直接写出所有符合条件的点P的坐标.
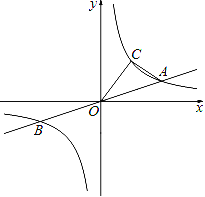
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校九年级共有450名学生,随机抽取其中的若干名学生,根据这些学生两次数学模拟考试成绩,分别绘制了如下所示的频数分布直方图,其中图②不完整.

注:① 成绩均为整数;②“60以下”不含60,其余分数段均包含端点;③ 图①、图②分别表示第一次、第二次模拟考试成绩频数分布直方图.
根据以上信息,解答下列问题:
(1)把图②补全;
(2)规定100分以上为优秀,请计算图②中达到优秀的比例;
(3)请你估算九年级学生第二次数学模拟考试达到优秀的人数比第一次数学模拟考试增加多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com