
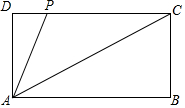
 如图,在矩形ABCD中,AB=2,BC=1,P在DC上,当AP=$\frac{\sqrt{5}}{2}$时,△ADP∽△ABC.
如图,在矩形ABCD中,AB=2,BC=1,P在DC上,当AP=$\frac{\sqrt{5}}{2}$时,△ADP∽△ABC. 分析 根据矩形的性质和相似三角形的对应边成比例求得AP的长度.
解答  解:∵在矩形ABCD中,AB=2,BC=1,
解:∵在矩形ABCD中,AB=2,BC=1,
∴AD=BC=1,AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{{2}^{2}+{1}^{1}}$=$\sqrt{5}$.
由△ADP∽△ABC得到:$\frac{AD}{AB}$=$\frac{AP}{AC}$,即$\frac{1}{2}$=$\frac{AD}{\sqrt{5}}$,
解得AD=$\frac{\sqrt{5}}{2}$.
故答案是:$\frac{\sqrt{5}}{2}$.
点评 本题考查了矩形的性质和相似三角形的判定.解题时,要找准相似三角形的对应边.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
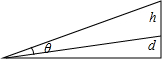 在一个艺术品陈列室内,一幅画的高度为h被悬挂于墙上,其底部边缘距离人的水平视线为d(如图),问人站在离墙多远欣赏这幅画最好?(换句话说怎样使得对应的θ最大)
在一个艺术品陈列室内,一幅画的高度为h被悬挂于墙上,其底部边缘距离人的水平视线为d(如图),问人站在离墙多远欣赏这幅画最好?(换句话说怎样使得对应的θ最大)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com