
【题目】已知:如图,在直角三角形ABC中,∠BAC=90°,AB=AC,D为BC的中点,E为AC上一点,点G在BE上,连接DG并延长交AE于F,若∠FGE=45°.

(1)求证:BDBC=BGBE;
(2)求证:AG⊥BE;
(3)若E为AC的中点,求EF:FD的值.
【答案】(1)(2)见解析(3)![]()
【解析】
试题(1)根据题意,易证△GBD∽△CBE,得![]() ,即BDBC=BGBE;
,即BDBC=BGBE;
(2)可通过证明ABG∽△EBA从而求得AG⊥BE;
(3)首先连接DE,E是AC中点,D是BC中点,得出DE∥BA,因为BA⊥AC,所以 DE⊥AC设AB=2a AE=a,做CH⊥BE交BE的延长线于H,再利用△AEG≌△CEH,以及△DEF∽△BHC得出即可.
试题解析:(1)证明:∵∠BAC=90°,AB=AC,∴∠ABC=∠C=45°.∵∠BGD=∠FGE=45°,∴∠C=∠BGD.∵∠GBC=∠GBC,∴△GBD∽△CBE,∴![]() ,即BDBC=BGBE;
,即BDBC=BGBE;
(2)证明:∵BDBC=BGBE,∠C=45°,∴BG=![]() =
=![]() =
=![]() =
=![]() ,∴
,∴![]() =
=![]() ,∠ABG=∠EBA,∴△ABG∽△EBA,∴∠BGA=∠BAE=90°,∴AG⊥BE;
,∠ABG=∠EBA,∴△ABG∽△EBA,∴∠BGA=∠BAE=90°,∴AG⊥BE;
(3)解:连接DE,连接DE,E是AC中点,D是BC中点,∴DE∥BA.∵BA⊥AC,∴DE⊥AC,设AB=2a AE=a,做CH⊥BE交BE的延长线于H.∵∠AEG=∠CEH,∠AGE=∠CHE,AE=EC,∴△AEG≌△CEH(AAS),∴CH=AG,∠GAE=∠HCE.∵∠BAE为直角,∴BE=![]() a,∴AG=AB×
a,∴AG=AB×![]() =
=![]() a=
a=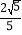 a,∴CH=
a,∴CH=![]() a.∵AG⊥BE,∠FGE=45°,∴∠AGF=45°=∠ECB.∵∠FGE=45°,∴∠AGE=90°,∴AG∥CH,∴∠GAE=∠HCE.∵∠DFE=∠GAE+∠AGF=∠HCE+∠ECB,∴∠DFE=∠BCH.又∵DE⊥AC,CH⊥BE,∴△DEF∽△BHC,∴EF:DF=CH:BC=
a.∵AG⊥BE,∠FGE=45°,∴∠AGF=45°=∠ECB.∵∠FGE=45°,∴∠AGE=90°,∴AG∥CH,∴∠GAE=∠HCE.∵∠DFE=∠GAE+∠AGF=∠HCE+∠ECB,∴∠DFE=∠BCH.又∵DE⊥AC,CH⊥BE,∴△DEF∽△BHC,∴EF:DF=CH:BC=![]() a:2
a:2![]() a=
a=![]() .
.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】小聪和小慧沿图l中的风景区游览,约好在飞瀑见面.小聪驾驶电动汽车从宾馆出发,小慧也于同一时间骑电动自行车从塔林出发.图2中的图像分别表示两人离宾馆的路程![]() 与时间
与时间![]() 的函数关系,试结合图中信息回答:
的函数关系,试结合图中信息回答:

(1)飞瀑与宾馆相距__________![]() ,小聪出发
,小聪出发![]() 时与宾馆的距离
时与宾馆的距离![]() _________
_________![]() ;
;
(2)若小聪出发![]() 后,速度变为小慧的2倍,则小聪追上小慧时,他们是否已经过了草甸?
后,速度变为小慧的2倍,则小聪追上小慧时,他们是否已经过了草甸?
(3)当出发多长时间时,两人相距![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图(1)).令△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图(2)),证明:MB=MC.
(2)若将图(1)中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图(3)),判断MB、MC的数量关系,并说明理由.
(3)在(2)中,若∠CAE的大小改变(图(4)),其他条件不变,则(2)中的MB、MC的数量关系还成立吗?说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,A(0,a),B(b,0)且a、b满足|a+2b﹣6|+|a﹣2b+2|=0.E为线段AB上一动点,∠BED=![]() ∠OAB,BD⊥EC,垂足在EC的延长线上,试求:
∠OAB,BD⊥EC,垂足在EC的延长线上,试求:

(1)判断△OAB的形状,并说明理由;
(2)如图1,当点E与点A重合时,探究线段AC与BD的数量关系,并证明你的结论;
(3)如图2,当点E在线段AB(不与A、B重合)上运动时,试探究线段EC与BD的数量关系,证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小红驾车从甲地到乙地,她出发第xh时距离乙地ykm,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y与x之间的函数关系.
(1)B点的坐标为( , );
(2)求线段AB所表示的y与x之间的函数表达式;
(3)小红休息结束后,以60km/h的速度行驶,则点D表示的实际意义是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:
是由两个小正方形和两个小长方形组成的,根据图形解答下列问题:

(1)请用两种不同的方法表示正方形![]() 的面积,并写成一个等式;
的面积,并写成一个等式;
(2)运用(1)中的等式,解决以下问题:
①已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
②已知![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() ,过顶点
,过顶点![]() 作射线
作射线![]() .
.
(1)当射线![]() 在
在![]() 外部时,如图①,点
外部时,如图①,点![]() 在射线
在射线![]() 上,连结
上,连结![]() 、
、![]() ,已知
,已知![]() ,
,![]() ,
,![]() (
(![]() ).
).
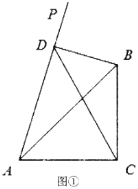
①试证明![]() 是直角三角形;
是直角三角形;
②求线段![]() 的长.(用含
的长.(用含![]() 的代数式表示)
的代数式表示)
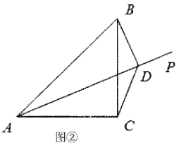
(2)当射线![]() 在
在![]() 内部时,如图②,过点
内部时,如图②,过点![]() 作
作![]() 于点
于点![]() ,连结
,连结![]() ,请写出线段
,请写出线段![]() 、
、![]() 、
、![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,图象(折线ABCDE)描述了一汽车在某一直路上行驶过程中汽车离出发地的距离S(千米)和行驶时间t(小时)之间的函数关系,根据图中提供的信息,下列说法正确的是( )

A.汽车共行驶了120千米
B.汽车在行驶途中停留了2小时
C.汽车在AB段的行驶速度与CD段的行驶速度相同
D.汽车自出发后3小时至4.5小时之间行驶的平均速度为80千米/时
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx(k≠0)沿着y轴向上平移3个单位长度后,与x轴交于点B(3,0),与y轴交于点C,抛物线y=x2+bx+c过点B、C且与x轴的另一个交点为A.
(1)求直线BC及该抛物线的表达式;
(2)设该抛物线的顶点为D,求△DBC的面积;
(3)如果点F在y轴上,且∠CDF=45°,求点F的坐标.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com