
【题目】如图,在坡角为30°的山坡上有一铁塔AB,其正前方矗立着一大型广告牌,当阳光与水平线成45°角时,测得铁塔AB落在斜坡上的影子BD的长为6米,落在广告牌上的影子CD的长为4米,求铁塔AB的高(AB,CD均与水平面垂直,结果保留根号).
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
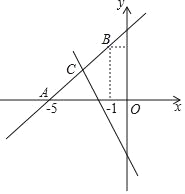
【题目】如图,直线y=kx+b经过点A(﹣5,0),B(﹣1,4).
(1)求直线AB的表达式;
(2)若直线y=﹣2x﹣4与直线AB相交于点C,求点C的坐标;
(3)根据图象,写出关于x的不等式kx+b>﹣2x﹣4的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条笔直的公路的同侧依次排列着A,C,B三个村庄,某天甲、乙两车分别从A,B两地出发,沿这条公路匀速行驶至C地停止,从甲车出发至甲车到达C地的过程,甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系如图所示.求: 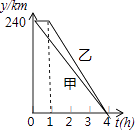
(1)甲的速度是 , 乙的速度是;
(2)分别求出甲、乙两车各自与C地的距离y(km)与甲车行驶时间t(h)之间的函数关系式,并写出取值范围;
(3)若甲、乙两车到C地后继续沿该公路原速度行驶,求甲车出发多少小时,两车相距350km.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,中线BE,CD相交于点O,连接DE,下列结论: ① ![]() =
= ![]() ;②
;② ![]() =
= ![]() ;③
;③ ![]() ;④
;④ ![]() =
= ![]()
其中正确的个数有( )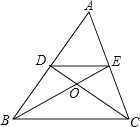
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,把∠α=60°的一个单独的菱形称作一个基本图形,将此基本图形不断的复制并平移,使得下一个菱形的一个顶点与前一个菱形的中线重合,这样得到图②,图③,… 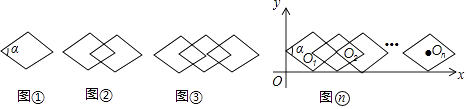
(1)观察以上图形并完成下表:
图形名称 | 基本图形的个数 | 菱形的个数 |
图① | 1 | 1 |
图② | 2 | 3 |
图③ | 3 | 7 |
图④ | 4 | |
… | … | … |
猜想:在图(n)中,菱形的个数为(用含有n(n≥3)的代数式表示);
(2)如图,将图(n)放在直角坐标系中,设其中第一个基本图的对称中心O1的坐标为(x1 , 1),则x1=;第2017个基本图形的中心O2017的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一个函数图象经过(1,﹣4),(2,﹣2)两点,在自变量x的某个取值范围内,都有函数值y随x的增大而减小,则符合上述条件的函数可能是( )
A.正比例函数
B.一次函数
C.反比例函数
D.二次函数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,O为原点,点A(﹣2,0),点B(0,2),点E,点F分别为OA,OB的中点.若正方形OEDF绕点O顺时针旋转,得正方形OE′D′F′,记旋转角为α. 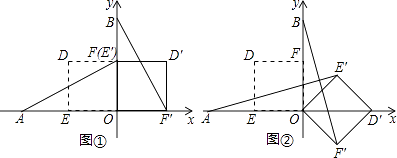
(Ⅰ)如图①,当α=90°时,求AE′,BF′的长;
(Ⅱ)如图②,当α=135°时,求证AE′=BF′,且AE′⊥BF′;
(Ⅲ)若直线AE′与直线BF′相交于点P,求点P的纵坐标的最大值(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2﹣4ax+3(a≠0)与y轴交于点A,A、B两点关于对称轴对称,直线OB分别与抛物线的对称轴相交于点C.
(1)直接写出对称轴及B点的坐标;
(2)已知直线y2=bx﹣4b+3(b≠0)与抛物线的对称轴相交于点D. ①判断直线y2=bx﹣4b+3(b≠0)是否经过点B,并说明理由;
②若△BDC的面积为1,求b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com