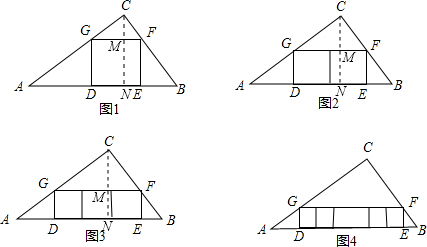
解:(1)在图1中作△ABC的高CN交GF于M,
在Rt△ABC中,∵AC=40,BC=30,∴AB=50,CN=24.
由GF∥AB,得△CGF∽△CAB,
∴
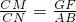
.
设正方形的边长为x,则
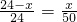
,
解得
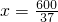
.
即正方形的边长为
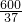
.
(2)方法同(1),如图2.
△CGF∽△CAB,则
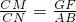
.
设小正方形的边长为x,
则
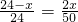
,
解得
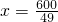
.
即小正方形的边长为
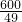
.
(3)在图3中,作CN⊥AB,交GF于点M,交AB于点N,
∵GF∥AB,∴△CGF∽△CAB,
∴
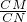
=
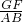
,
设每个正方形的边长为x,
则
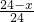
=
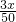
,
∴x=
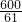
;
(4)设每个正方形的边长为x,同理得到:
则
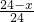
=
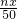
,
则x=
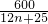
.
∴每个小正方形的边长为
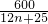
.
分析:(1)根据题意画出图形,作CN⊥AB,再根据GF∥AB,可知△CGF∽△CAB,由平行得到两对同位角相等,进而得到两三角形相似,设出正方形的边长为x,根据相似三角形的性质得到比例式,进而列出关于x的方程,求出方程的解,即可求出正方形的边长;
(2)作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比,同理可求出正方形的边长;
(3)作CN⊥AB,交GF于点M,交AB于点N,同(1)可知,△CGF∽△CAB,根据对应边的比等于相似比,同理可求出正方形的边长;
(4)同理可得正方形的边长.
点评:此题综合考查了正方形、矩形、相似三角形的性质及勾股定理.要求学生掌握相似三角形的对应高之比等于相似比,注意此题虽有四问,但是方法雷同,只是比例式中GF代入的式子不同,应根据图形正方形的个数来确定.


 解:(1)在图1中作△ABC的高CN交GF于M,
解:(1)在图1中作△ABC的高CN交GF于M,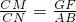 .
.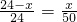 ,
,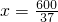 .
.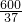 .
.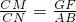 .
.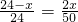 ,
,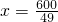 .
.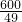 .
.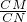 =
=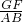 ,
,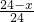 =
=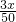 ,
,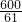 ;
;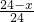 =
=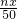 ,
,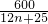 .
.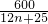 .
.

 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
