
分析 (1)令x+2=0,x-4=0求得x的值即可;
(2)分为x<-2、-2≤x<4,x≥4三种情况化简计算即可;
(3)根据(2)中的化简结果列方程求解即可.
解答 解:(1)分别令x+2=0,x-4=0,解得:x=-2和x=4
所以|x+2|和|x-4|的零点值分别为x=-2和x=4;
(2)当x<-2时,原式=-(x+2)-(x-4)=-2x+2;
当-2≤x<4时,原式=x+2-(x-4)=6;
当x≥4时,原式=x+2+x-4=2x-2.
综上讨论,原式=$\left\{\begin{array}{l}{-2x+2(x<-2)}\\{6(-2≤x<4)}\\{2x-2(x≥4)}\end{array}\right.$
(3)当x<-2时,-2x+2=8,解得x=-3;
当x≥4时,2x-2=8,解得:x=5.
所以原方程的解为x=-3或x=5.
点评 本题主要考查的是化简绝对值,分类讨论是解题的关键.


科目:初中数学 来源: 题型:填空题
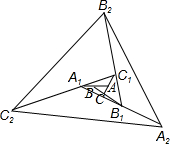 如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为142015.
如图,△ABC面积为1,第一次操作:分别延长AB,BC,CA至点A1,B1,C1,使A1B=AB、B1C=2BC,C1A=2CA,顺次连接A1,B1,C1,得到△A1B1C1.第二次操作:分别延长A1B1,B1C1、C1A1至点A2,B2,C2,使A2B1=A1B1,B2C1=2B1C1,C2A1=2C1A1,顺次连接A2,B2,C2,得到△A2B2C2,…按此规律,经过2015次操作后△A2015B2015C2015的面积为142015.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com