
【题目】如图,已知正方形ABCD,点E是边AB的中点,点O是线段AE上的一个动点(不与A、E重合),以O为圆心,OB为半径的圆与边AD相交于点M,过点M作⊙O的切线交DC于点N,连接OM、ON、BM、BN.记△MNO、△AOM、△DMN的面积分别为S1、S2、S3,则下列结论不一定成立的是( )

A.S1>S2+S3 B.△AOM∽△DMN C.∠MBN=45° D.MN=AM+CN
【答案】A.
【解析】
试题(1)如答图1,过点M作MP∥AO交ON于点P,
∵点O是线段AE上的一个动点,
当AM=MD时,S梯形ONDA=![]() (OA+DN)ADS△MNO=
(OA+DN)ADS△MNO=![]() MPAD,
MPAD,
∵![]() (OA+DN)=MP,∴S△MNO=
(OA+DN)=MP,∴S△MNO=![]() S梯形ONDA,
S梯形ONDA,
∴S1=S2+S3,∴不一定有S1>S2+S3. 故A不一定成立.

(2)∵MN是⊙O的切线,∴OM⊥MN,
又∵四边形ABCD为正方形,
∴∠A=∠D=90°,∠AMO+∠DMN=90°,∠AMO+∠AOM=90°.∴∠AOM=∠DMN.
在△AMO和△DMN中,∵![]() ,∴△AMO∽△DMN.故B成立.
,∴△AMO∽△DMN.故B成立.
(3)如答图2,过点B作BP⊥MN于点P,
∵MN,BC是⊙O的切线,
∴∠PMB=![]() ∠MOB,∠CBM=
∠MOB,∠CBM=![]() ∠MOB.
∠MOB.
∵AD∥BC,∴∠CBM=∠AMB. ∴∠AMB=∠PMB.
在Rt△MAB和Rt△MPB中,∵ ,
,
∴Rt△MAB≌Rt△MPB(AAS).∴AM=MP,∠ABM=∠MBP,BP=AB=BC.
在Rt△BPN和Rt△BCN中,![]() ,∴Rt△BPN≌Rt△BCN(HL).
,∴Rt△BPN≌Rt△BCN(HL).
∴PN=CN,∠PBN=∠CBN. ∴∠MBN=∠MBP+∠PBN.
∴MN=MN+PN=AM+CN.故C,D成立.
综上所述,A不一定成立.
故选A.



 应用题作业本系列答案
应用题作业本系列答案科目:初中数学 来源: 题型:
【题目】《九章算术》记载“今有邑方不知大小,各中开门.出北门三十步有木,出西门七百五十步见木.问邑方有几何?”意思是:如图,点M、点N分别是正方形ABCD的边AD、AB的中点,ME⊥AD,NF⊥AB,EF过点A,且ME=30步,NF=750步,则正方形的边长为( )
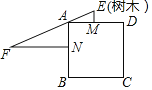
A. 150步B. 200步C. 250步D. 300步
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,那么,当以A、P、Q为顶点的三角形与△ABC相似时,运动时间为_________________
|
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点都在格点上.

(1)请按下列要求画图:
①将△ABC先向右平移5个单位,再向上平移1个单位,得到△A1B1C1,画出△A1B1C1;
②△A2B2C2与△ABC关于原点O成中心对称,画出△A2B2C2;
(2)若(1)所得的△A1B1C1与△A2B2C2,关于点P成中心对称,直接写出对称中心P点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形![]() 中,对角线
中,对角线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 为
为![]() 上动点(不与
上动点(不与![]() 、
、![]() 重合),作
重合),作![]() ,垂足为
,垂足为![]() ,分别交
,分别交![]() 、
、![]() 于
于![]() 、
、![]() ,连接
,连接![]() 、
、![]() .
.

(1)求证:![]() ;
;
(2)求![]() 的度数;
的度数;
(3)若![]() ,
,![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
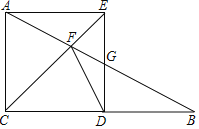
【题目】在Rt△ABC中,∠ACB=90°,AC=12.点D在直线CB上,以CA,CD为边作矩形ACDE,直线AB与直线CE,DE的交点分别为F,G,
(1)如图,点D在线段CB上,四边形ACDE是正方形.
①若点G为DE的中点,求FG的长.
②若DG=GF,求BC的长.
(2)已知BC=9,是否存在点D,使得△DFG是等腰三角形?若存在,求该三角形的腰长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=-x2+bx+c的图象经过A(-2,-1),B(0,7)两点.

(1)求该抛物线的解析式及对称轴;
(2)当x为何值时,y>0?
(3)在x轴上方作平行于x轴的直线l,与抛物线交于C,D两点(点C在对称轴的左侧),过点C,D作x轴的垂线,垂足分别为F,E.当矩形CDEF为正方形时,求C点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
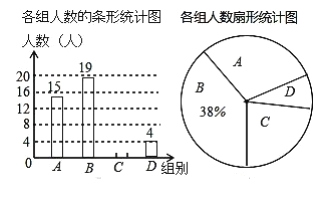
【题目】近年来我市大力发展绿色交通,构建公共、绿色交通体系,将“共享单车”陆续放置在人口流量较大的地方,琪琪同学随机调查了若干市民租用“共享单车”的骑车时间![]() (单位:分),将获得的数据分成四组,绘制了如下统计图(
(单位:分),将获得的数据分成四组,绘制了如下统计图(![]() ),根据图中信息,解答下列问题:
),根据图中信息,解答下列问题:
(1)这项被调查的总人数是 人,表示![]() 组的扇形统计图的圆心角的度数为 .
组的扇形统计图的圆心角的度数为 .
(2)若某小区共有![]() 人,根据调查结果,估计租用“共享单车”的骑车时间为
人,根据调查结果,估计租用“共享单车”的骑车时间为![]() 的大约有多少人?
的大约有多少人?
(3)如果琪琪同学想从![]() 组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
组的甲、乙、丙、丁四人中随机选择两人了解平时租用“共享单车”的骑车时间情况,请用列表或画树状图的方法求出恰好选中甲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
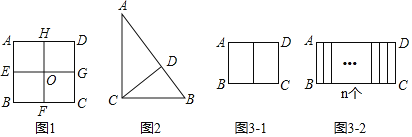
【题目】阅读下列材料,完成任务:
自相似图形,定义:若某个图形可分割为若干个都与它相似的图形,则称这个图形是自相似图形.例如:正方形ABCD中,点E、F、G、H分别是AB、BC、CD、DA边的中点,连接EG,HF交于点O,易知分割成的四个四边形AEOH、EBFO、OFCG、HOGD均为正方形,且与原正方形相似,故正方形是自相似图形.
(1)图1中正方形ABCD分割成的四个小正方形中,每个正方形与原正方形的相似比为______;
(2)如图2,已知△ABC中,∠ACB=90°,AC=4,BC=3,小明发现△ABC也是“自相似图形”,他的思路是:过点C作CD⊥AB于点D,则CD将△ABC分割成2个与它自己相似的小直角三角形.则△ACD与△ABC的相似比为_____;则△BCD与△ABC的相似比为_____;
(3)现有一个矩形ABCD是自相似图形,其中长AD=a,宽AB=b(a>b).
①如图3﹣1,若将矩形ABCD纵向分割成两个全等矩形,且与原矩形都相似,则a=_____(用含b的式子表示):
②如图3﹣2,若将矩形ABCD纵向分割成n个全等矩形,且与原矩形都相似,则a=______(用含n,b的式子表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com