
【题目】如图,点P为△ABC三边垂直平分线的交点,∠PAC=20°,∠PCB=30°,

(1)求∠PAB的度数;
(2)直接写出∠APB与∠ACB的数量关系 .
【答案】(1)∠PAB=40°;(2)∠APB=2∠ACB.
【解析】
(1)由P为△ABC三边垂直平分线的交点,推出PA=PC=PB,由等腰三角形的性质证得∠PAC=∠PCA=20°,∠PBC=∠PCN=30°,由∠PAB=∠PBA,根据三角形的内角和即可推出结论;
(2)分别计算两角的大小,从而得出两角的数量关系.
(1)∵P为△ABC三边垂直平分线的交点,
∴PA=PC=PB,
∴∠PAC=∠PCA=20°,
∠PBC=∠PCN=30°,
∵∠PAB=∠PBA,
∴∠PAB=![]() (180°﹣2×20°﹣2×30°)=40°.
(180°﹣2×20°﹣2×30°)=40°.
(2)∵∠APB=180°﹣40°﹣40°=100°,∠ACB=∠ACP+∠PCB=50°,
∴∠APB=2∠ACB.
故答案为∠APB=2∠ACB.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:初中数学 来源: 题型:
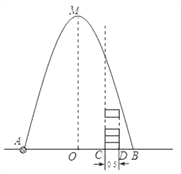
【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,已知点![]() ,
,![]() 与坐标原点O在同一直线上,且AO=BO,其中m,n满足
与坐标原点O在同一直线上,且AO=BO,其中m,n满足![]() .
.
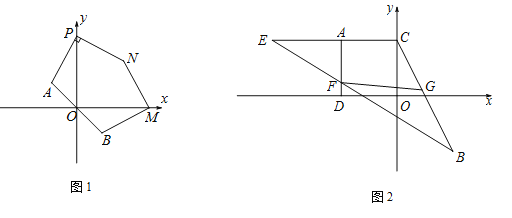
(1)求点A,B的坐标;
(2)如图1,若点M,P分别是x轴正半轴和y轴正半轴上的点,点P的纵坐标不等于2,点N在第一象限内,且![]() ,PA⊥PN,
,PA⊥PN,![]() ,求证:BM⊥MN;
,求证:BM⊥MN;
(3)如图2,作AC⊥y轴于点C,AD⊥x轴于点D,在CA延长线上取一点E,使![]() ,连结BE交AD于点F,恰好有
,连结BE交AD于点F,恰好有![]() ,点G是CB上一点,且
,点G是CB上一点,且![]() ,连结FG,求证:
,连结FG,求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠C=90°.

(1)在斜边AB上确定一点E,使点E到点B距离和点E到AC的距离相等;(要求:尺规作图,不写作法,保留作图痕迹)
(2)在(1)的条件下,若BC=6,AC=8,点E到AC的距离为ED,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某气球内充满一定质量的气体,当温度不变时,气球内气体的气压p(kPa)是气体体积V(m3)的反比例函数,其图象如图所示.

(1)写出这一函数的表达式.
(2)当气体体积为1 m3时,气压是多少?
(3)当气球内的气压大于140 kPa时,气球将爆炸,为了安全考虑,气体的体积应不小于多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在同一平面内,若一个点到一条直线的距离不大于1,则称这个点是该直线的“伴侣点”.
在平面直角坐标系中,已知点M(1,0),过点M作直线l平行于y轴,点A(﹣1,a),点B(b,2a),点 C(﹣![]() ,a﹣1),将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.
,a﹣1),将三角形ABC进行平移,平移后点A的对应点为D,点B的对应点为E,点C的对应点为F.
(1)试判断点A是否是直线l的“伴侣点”?请说明理由;
(2)若点F刚好落在直线l上,F的纵坐标为a+b,点E落在x轴上,且三角形MFD的面积为![]() ,试判断点B是否是直线l的“伴侣点”?请说明理由.
,试判断点B是否是直线l的“伴侣点”?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com