解答:解:(Ⅰ)设时间为t,则AP=BQ=t,PB=4-t
①当∠PQB=90°时,∵∠B=60°,∴PB=2BQ,得4-t=2t,解得,t=
;
②当∠BPQ=90°,∵∠B=60°,∴BQ=2PB,得t=2(4-t),解得t=
;
∴当AP=
cm或AP=
cm时,△PBQ为直角三角形--------------------------(4分)
(Ⅱ)①当点P,Q分别在线段AB,BC上运动时,∠CMQ=60°不变.
∵等边△ABC中,AB=AC,∠B=∠CAP=60°,
又由条件得AP=BQ,∴△ABQ≌△CAP(SAS),
∴∠BAQ=∠ACP(全等三角形的对应角相等),
∴∠CMQ=∠ACP+∠CAM=∠BAQ+∠CAM=∠BAC=60°--------(6分)
②当点P,Q分别在射线AB,BC上运动时,∠CMQ=120°不变.
∵在等边△ABC中,AB=AC,∠B=∠CAP=60°,
∴∠PBC=∠ACQ=120°,又由条件得BP=CQ,
∴△PBC≌△ACQ(SAS),
∴∠BPC=∠MQC(全等三角形的对应角相等),
又∵∠PCB=∠MCQ,
∴∠CMQ=∠PBC=120°(等量代换)-------------------------------------------------------------(10分)




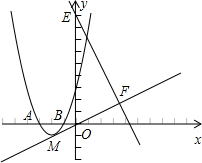 (Ⅰ)求抛物线C的解析式;
(Ⅰ)求抛物线C的解析式;