
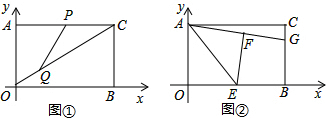
分析 (1)分CQ=CP、PC=PQ和QC=PQ三种情况,根据等腰三角形的性质计算即可;
(2)连接EG,由翻转变换的性质得到△AOE≌△AFE,根据全等三角形的性质得到∠EFG=∠OBC=90°,证明Rt△EFG≌Rt△EBG得到∠FEG=∠BEG,∠AOB=∠AEG=90°,得到△AOE∽△AEG,根据相似三角形的性质列出比例式,计算即可.
解答 解:(1)设运动的时间为t秒,
由勾股定理得,OC=$\sqrt{O{A}^{2}+A{C}^{2}}$=10,
当CQ=CP时,2t=10-4t,
解得,t=$\frac{5}{3}$,
此时CP=2×$\frac{5}{3}$=$\frac{10}{3}$,
∴AP=8-$\frac{10}{3}$=$\frac{14}{3}$,
P点坐标为($\frac{14}{3}$,6),
当PC=PQ时,
如图①,过点Q作AC的垂线交AC于点E,CQ=10-4t,CP=2t.
∵△CEQ∽△CAO,
∴EQ=$\frac{3}{5}$CQ=$\frac{3}{5}$(10-4t)=6-$\frac{12}{5}$t,PE=$\frac{4}{5}$(10-4t)-2t=8-$\frac{16}{5}$t-2t=8-$\frac{26}{5}$t,
由勾股定理得,(6-$\frac{12}{5}$t)2+(8-$\frac{26}{5}$t)2=(2t)2,
整理得:36t2-140t+125=0,
解得,t1=$\frac{25}{18}$,t2=$\frac{5}{2}$(舍去),
此时,AP=8×$\frac{25}{18}$×2=$\frac{47}{9}$,
∴P点坐标为($\frac{47}{9}$,6),
当QC=PQ时,如图②,过点Q作AC的垂线交AC于点F,
CQ=10-4t,CP=2t,
∵△CFQ∽△CAO,
∴QF═$\frac{3}{5}$(10-4t)=6-$\frac{12}{5}$t,PF=2t-$\frac{4}{5}$(10-4t)=$\frac{26}{5}$t-8,
则(6-$\frac{12}{5}$t)2+($\frac{26}{5}$t-8)2=(10-4t)2,
整理得,21t2-40t=0,
解得,t1=$\frac{40}{21}$,t2=0(舍去),
此时,AP=8-$\frac{40}{21}$×2=$\frac{88}{21}$,
则P点坐标为($\frac{88}{21}$,6),
综上所述,P点坐标为($\frac{14}{3}$,6),($\frac{47}{9}$,6),($\frac{88}{21}$,6);
(2))如图③,连接EG,
由题意得:△AOE≌△AFE,
∴∠EFG=∠OBC=90°,
∵E是OB的中点,
∴EG=EG,EF=EB=4,
在Rt△EFG和Rt△EBG中,
$\left\{\begin{array}{l}{EF=EB}\\{EG=EG}\end{array}\right.$,
∴Rt△EFG≌Rt△EBG(HL)
∴∠FEG=∠BEG,∠AOB=∠AEG=90°,
∴△AOE∽△AEG,
∴AE2=AO•AG,
即36+16=6×AG,
解得,AG=$\frac{26}{3}$,
由勾股定理得,CG=$\sqrt{A{G}^{2}-A{C}^{2}}$=$\frac{10}{3}$,
∴BG=6-$\frac{10}{3}$=$\frac{8}{3}$,
G的坐标为(8,$\frac{8}{3}$).
点评 本题考查的是翻转变换的性质、等腰三角形的性质、相似三角形的判定和性质,掌握翻转变换的性质、灵活运用分情况讨论思想是解题的关键.


科目:初中数学 来源: 题型:解答题
 如图,AB∥CD,AB=1,CD=4,BC=3,AD=4.
如图,AB∥CD,AB=1,CD=4,BC=3,AD=4.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 三角形按边分可分为不等边三角形、等腰三角形 | |
| B. | 等腰三角形的内角可能是钝角或直角 | |
| C. | 三角形外角一定是钝角 | |
| D. | 三角形的中线把三角形分成面积相等的两部分 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
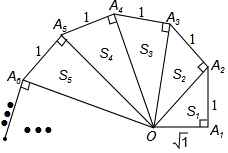 细心观察图形,认真分析各式,然后解答问题.
细心观察图形,认真分析各式,然后解答问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com