
 体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.
体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.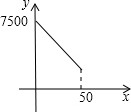 解:(1)设三人间有a间,双人间有b间.根据题意得
解:(1)设三人间有a间,双人间有b间.根据题意得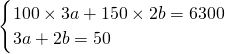 .
.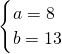 .
. 、
、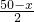 为整数值的增大值时,即x=48时,住宿费用最低.
为整数值的增大值时,即x=48时,住宿费用最低.

科目:初中数学 来源: 题型:
 体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.
体入住一律五折优惠.一个50人的旅游团在十月二号到该酒店住宿,租住了一些三人间,双人间客房.查看答案和解析>>
科目:初中数学 来源:广东省期末题 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com