
【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
科目:初中数学 来源: 题型:
【题目】在ABCD中,点E,F分别在边BC,AD上,且AF=CE.

(Ⅰ)如图①,求证四边形AECF是平行四边形;
(Ⅱ)如图②,若∠BAC=90°,且四边形AECF是边长为6的菱形,求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四边形ABCD中,E、F分别是边BC、CD的中点,连接AE,AF.
(1)如图1,若四边形ABCD的面积为5,则四边形AECF的面积为____________;
(2)如图2,延长AE至G,使EG=AE,延长AF至H,使FH=AF,连接BG、GH、HD、DB.
求证:四边形BGHD是平行四边形;
(3)如图3,对角线 AC、BD相交于点M, AE与BD交于点P, AF与BD交于点N. 直接写出BP、PM、MN、ND的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了加强训练学生的篮球和足球运球技能,准备购买一批篮球和足球用于训练,已知1个篮球和2个足球共需116元;2个篮球和3个足球共需204元
![]() 求购买1个篮球和1个足球各需多少元?
求购买1个篮球和1个足球各需多少元?
![]() 若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
若学校准备购进篮球和足球共40个,并且总费用不超过1800元,则篮球最多可购买多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,∠CAB=50°.按以下步骤作图:①以点A为圆心,小于AC的长为半径画弧,分别交AB、AC于点E、F;②分别以点E、F为圆心,大于 ![]() EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 .
EF的长为半径画弧,两弧相交于点G;③作射线AG交BC边于点D.则∠ADC的度数为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,∠B=30°,BC=3.点D是BC边上的一动点(不与点B、C重合),过点D作DE⊥BC交AB于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处.当△AEF为直角三角形时,BD的长为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,钝角△ABC.

(1)过A作AE⊥BC,过B作BF⊥AC,垂足分别为E,F,AE,BF相交于H;
(2)过A作AM∥BC,过B作BM∥AC,相交于M;
(3)若∠AMB=115°,求∠AHB.
查看答案和解析>>
科目:初中数学 来源: 题型:
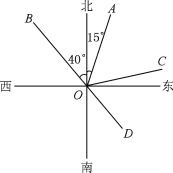
【题目】如图,射线OA表示的方向是北偏东15°,射线OB表示的方向是北偏西40°.
(1)若∠AOC=∠AOB,则射线OC表示的方向是 ;
(2)若射线OD是射线OB的反向延长线,则射线OD表示的方向是 ;
(3)∠BOD可以看作是由OB绕点O逆时针方向旋转至OD形成的角,作∠BOD的平分线OE;
(4)在(1),(2),(3)的条件下,求∠COE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图在坐标系中放置一菱形OABC,已知∠ABC=60°,点B在y轴上,OA=1,先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2017次,点B的落点依次为B1 , B2 , B3 , …,则B2017的坐标为( ) 
A.(1345,0)
B.(1345.5, ![]() )
)
C.(1345, ![]() )
)
D.(1345.5,0)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com