
【题目】点![]() 在数轴上所对应的数分别是
在数轴上所对应的数分别是![]() ,其中
,其中![]() 满足
满足![]() .
.
(1)求![]() 的值;
的值;
(2)数轴上有一点![]() ,使得
,使得![]() ,求点
,求点![]() 所对应的数;
所对应的数;
(3)点![]() 为
为![]() 中点,
中点,![]() 为原点,数轴上有一动点
为原点,数轴上有一动点![]() ,求
,求![]() 的最小值及点
的最小值及点![]() 所对应的数的取值范围.
所对应的数的取值范围.
【答案】(1)![]() ;(2)点
;(2)点![]() 所对应的数为
所对应的数为![]() 或
或![]() ;(3)设点P所表示的数为p,当-6≤p≤-1时,
;(3)设点P所表示的数为p,当-6≤p≤-1时,![]() 最小,且最小值为9
最小,且最小值为9
【解析】
(1)根据平方和绝对值的非负性即可求出a、b的值;
(2)先求出AB的值,设点C表示的数为c,然后根据点C的位置分类讨论,分别画出图形,利用含c的式子表示出AC和BC,列出对应的方程即可求出;
(3)根据中点公式求出点D所表示的数,设点P所表示的数为p,根据点P与点O的相对位置分类讨论,画出相关的图形,分析每种情况下![]() 取最小值时,点P的位置即可.
取最小值时,点P的位置即可.
解:(1)∵![]() ,
,![]()
∴![]()
解得:![]() ;
;
(2)由(1)可得:AB=4-(-6)=10
设点C表示的数为c
①当点C在点B左侧时,如下图所示

∴AC=4-c,BC=-6-c
∵![]()
∴![]()
解得:c=![]() ;
;
②当点C在线段AB上时,如下图所示:
![]()
此时AC+BC=AB
故不成立;
③当点C在点A右侧时,如下图所示

∴AC=c-4,BC= c -(-6)=c+6
∵![]()
∴![]()
解得:c=![]() ;
;
综上所述:点![]() 所对应的数为
所对应的数为![]() 或
或![]() ;
;
(3)∵点D为AB的中点
所以点D表示的数为![]()
设点P所表示的数为p
①当点P在点O左侧时,如以下三个图所示,此时PA-PO=AO=4
∴![]()
即当![]() 取最小值时,
取最小值时,![]() 也最小
也最小
由以下三个图可知:当点P在线段BD上时,![]() 最小,此时
最小,此时![]()



∴此时![]()
即当-6≤p≤-1时,![]() 最小,且最小值为9;
最小,且最小值为9;
②当点P在点O右侧时,如以下两个图所示,此时PB-PO=OB=6
∴![]()
即当![]() 取最小值时,
取最小值时,![]() 也最小
也最小
由以下两个图可知:当点P在线段OA上时,![]() 最小,此时
最小,此时![]()


∴此时![]()
即当0≤p≤4时,![]() 最小,且最小值为11;
最小,且最小值为11;
综上所述:当-6≤p≤-1时,![]() 最小,且最小值为9.
最小,且最小值为9.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:
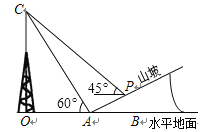
【题目】如图所示,某人在山坡坡脚A处测得电视塔尖点C 的仰角为60°,沿山坡向上走到P处再测得C的仰角为45°,已知OA=200米,山坡坡度为![]() (即tan∠PAB=
(即tan∠PAB=![]() ),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
),且O、A、B在同一条直线上,求电视塔OC的高度以及此人所在位置点P的垂直高度.(测倾器的高度忽略不计,结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为 4 的等边△ABC 中,点 D 从点A 开始在射线 AB 上运动,速度为 1 个单位/秒,点F 同时从 C 出发,以相同的速度沿射线 BC 方向运动,过点D 作 DE⊥AC,连结 DF 交射线 AC 于点 G
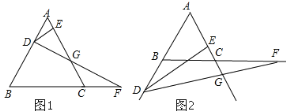
(1)当 DF⊥AB 时,求 t 的值;
(2)当点 D 在线段 AB 上运动时,是否始终有 DG=GF?若成立,请说明理由。
(3)聪明的斯扬同学通过测量发现,当点 D 在线段 AB 上时,EG 的长始终等于 AC 的一半,他想当点D 运动到图 2 的情况时,EG 的长是否发生变化?若改变,说明理由;若不变,求出 EG 的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,某学校计划租用![]() 辆客车送
辆客车送![]() 名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车
名师生参加研学活动,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车![]() 辆,租车总费用为
辆,租车总费用为![]() 元.
元.
甲种客车 | 乙种客车 | |
载客量(人/辆) |
|
|
租金(元/辆) |
|
|
(1)求出![]() (元)与
(元)与![]() (辆)之间函数关系式;
(辆)之间函数关系式;
(2)求出自变量的取值范围;
(3)选择怎样的租车方案所需的费用最低?最低费用多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公交公司有A,B型两种客车,它们的载客量和租金如下表:
A | B | |
载客量(人/辆) | 45 | 30 |
租金(元/辆) | 400 | 280 |
红星中学根据实际情况,计划租用A,B型客车共5辆,同时送七年级师生到基地参加社会实践活动,设租用A型客车x辆,根据要求回答下列问题:
(1)用含x的式子填写下表:
车辆数(辆) | 载客量(人) | 租金(元) | |
A | x | 45x | 400x |
B | 5-x |
(2)若要保证租车费用不超过1900元,求x的最大值;
(3)在(2)的条件下,若七年级师生共有195人,写出所有可能的租车方案,并确定最省钱的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】[阅读理解]射线![]() 是
是![]() 内部的一条射线,若
内部的一条射线,若![]() 则我们称射线
则我们称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
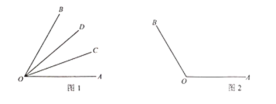
例如,如图1,![]() ,则
,则![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线:同时,由于
的伴随线:同时,由于![]() ,称射线
,称射线![]() 是射线
是射线![]() 的伴随线.
的伴随线.
[知识运用]
(1)如图2,![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,则
的伴随线,则![]() ,若
,若![]() 的度数是
的度数是![]() ,射线
,射线![]() 是射线
是射线![]() 的伴随线,射线
的伴随线,射线![]() 是
是![]() 的平分线,则
的平分线,则![]() 的度数是 .(用含
的度数是 .(用含![]() 的代数式表示)
的代数式表示)
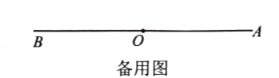
(2)如图,如![]() ,射线
,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度逆时针旋转,射线
的速度逆时针旋转,射线![]() 与射线
与射线![]() 重合,并绕点
重合,并绕点![]() 以每秒
以每秒![]() 的速度顺时针旋转,当射线
的速度顺时针旋转,当射线![]() 与射线
与射线![]() 重合时,运动停止,现在两射线同时开始旋转.
重合时,运动停止,现在两射线同时开始旋转.

①是否存在某个时刻![]() (秒),使得
(秒),使得![]() 的度数是
的度数是![]() ,若存在,求出
,若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
②当![]() 为多少秒时,射线
为多少秒时,射线![]() 中恰好有一条射线是其余两条射线的伴随线.
中恰好有一条射线是其余两条射线的伴随线.
查看答案和解析>>
科目:初中数学 来源: 题型:
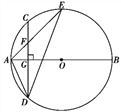
【题目】如图,AB是☉O的直径,弦CD⊥AB于点G,点F是CD上一点,且满足![]() =
=![]() ,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=
,连接AF并延长交☉O于点E,连接AD、DE,若CF=2,AF=3.给出下列结论:①△ADF∽△AED;②FG=3;③tan∠E=![]() ;④S△ADF=6
;④S△ADF=6![]() .
.
其中正确结论的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】出租车司机小王某天下午营运的路线全是在东西走向的大道上,小王从点![]() 出发,如果规定向东为正,向西为负,他这天下午的行驶记录如下:+5,-3,-8,-6,+10,-6,+12,-10(单位:千米)
出发,如果规定向东为正,向西为负,他这天下午的行驶记录如下:+5,-3,-8,-6,+10,-6,+12,-10(单位:千米)
(1)将最后一名乘客送到目的地时,小王距离出发点![]() 是多少千米?在点
是多少千米?在点![]() 的哪个方向?
的哪个方向?
(2)若汽车耗油量为![]() 升/千米,小王送完最后一个乘客后回到出发点
升/千米,小王送完最后一个乘客后回到出发点![]() ,共耗油多少升?(用含
,共耗油多少升?(用含![]() 的代数式表示)
的代数式表示)
(3)出租车油箱内原有12升油,请问:当![]() 时,小王途中是否需要加油?若需要加油,至少需要加多少升油?如不需要,说明理由.
时,小王途中是否需要加油?若需要加油,至少需要加多少升油?如不需要,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把一副三角板如图甲放置,其中∠ACB=∠DEC=90°,∠A=45°,∠D=30°,斜边AB=6,DC=7,把三角板DCE绕点C顺时针旋转15°得到△D1CE1(如图乙),此时AB与CD1交于点O,则线段AD1的长为( )
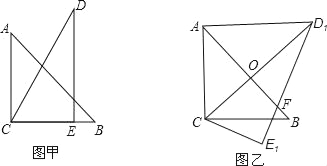
A. ![]() B. 5 C. 4 D.
B. 5 C. 4 D. ![]()
【答案】B
【解析】由旋转的性质可知,在图乙中,∠BCE1=15°,∠D1CE1=60°,AB=6,CD1=CD=7,
∴∠D1CB=60°-15°=45°,
又∵∠ACB=90°,
∴CO平分∠ACB,
又∵AC=BC,
∴CO⊥AB,且CO=AO=BO=![]() AB=3,
AB=3,
∴D1O=CD1-CO=7-3=4,∠AOD1=90°,
∴在Rt△AOD1中,AD1=![]() .
.
故选B.
点睛:本题解题的关键是由旋转的性质证明:∠D1CB=45°,从而得到CD1平分∠ACB,结合等腰三角形的“三线合一”证得∠AOD1=90°,并求得AO=3,OD1=4;这样问题就变得很简单了.
【题型】单选题
【结束】
10
【题目】我市某小区实施供暖改造工程,现甲、乙两工程队分别同时开挖两条600米长的管道,所挖管道长度y(米)与挖掘时间x(天)之间的关系如图所示,则下列说法中,正确的个数有( )个.
①甲队每天挖100米;
②乙队开挖两天后,每天挖50米;
③当x=4时,甲、乙两队所挖管道长度相同;
④甲队比乙队提前2天完成任务.
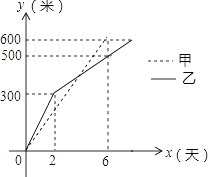
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com