
【题目】如图,⊙O为△ABC的外接圆,AB=AC,直线MN与⊙O相切于点C,弦BD∥MN,AC与BD相交于点E.

(1)求证:△ABE ≌ △ACD;
(2)若AB = 5,BC = 3,求AE.
【答案】(1) 见解析;(2) AE = ![]() .
.
【解析】分析:(1)在两个三角形中,证明两个三角形全等,找出三角形全等的条件,根据同弧所对的圆周角相等,根据所给的边长相等,由边角边确定两个三角形是全等三角形.
(2)可以证明![]() 得到对应边成比例,设出要求的边长,得到关于边长的方程,解方程即可.
得到对应边成比例,设出要求的边长,得到关于边长的方程,解方程即可.
详解:(1)连接OC,
∵直线MN与⊙O相切于点C,
∴OC ⊥ MN,
∵BD∥ MN,
∴OC ⊥ BD,
∴ ![]() =
=![]() ,
,
∴∠BAE =∠CAD,
在△ABE和△ACD中
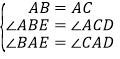
∴△ABE ≌ △ACD(ASA).
(2)由(1)知∠BAC = ∠CAD = ∠CBD,
∴![]()
∴![]() ,
,
∵![]() ,
,
∴CE = ![]() ,
,
∴AE = ![]() .
.


科目:初中数学 来源: 题型:
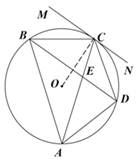
【题目】将连续的奇数1、3、5、7、9、…排成如图的数表,根据题意解答下列问题:
(1)通过观察十字框中5个数的和与中间23满足的关系,发现:若将十字框上下左右平移,可框住另外的5个数也有同样的规律请说出这个规律.
(2)十字框中5个数的和能等于425吗?若能,请写出这5个数,若不能,说明理由.
(3)十字框中5个数的和能等于2020吗?请说明理由;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧;
,按如图1所示摆放,将OA、OC边重合在直线MN上,OB、OD边在直线MN的两侧;



(1)保持![]() 不动,将
不动,将![]() 绕点O旋转至如图2所示的位置,则①
绕点O旋转至如图2所示的位置,则①![]() = ;②
= ;②![]() = ;
= ;
(2)若![]() 按每分钟
按每分钟![]() 的速度绕点O逆时针方向旋转,
的速度绕点O逆时针方向旋转,![]() 按每分钟
按每分钟![]() 的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算
的速度也绕点O逆时针方向旋转,OC旋转到射线ON上时都停止运动,设旋转t分钟,计算![]() (用t的代数式表示)。
(用t的代数式表示)。
(3)保持![]() 不动,将
不动,将![]() 绕点O逆时针方向旋转
绕点O逆时针方向旋转![]() ,若射线OE平分
,若射线OE平分![]() ,射线OF平分
,射线OF平分![]() ,求
,求![]() 的大小;
的大小;
查看答案和解析>>
科目:初中数学 来源: 题型:
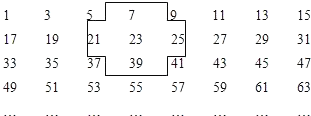
【题目】在求两位数乘两位数时,可以用“列竖式”的方法进行速算,如图给出了部分速算过程.
(1)根据前3个“列竖式”的速算方法,可得a=_____,b=_____,c=_____,d=_____,e=_____,f=_____;
(2)根据前3个“列竖式”的速算方法,在速算“31×![]() ”时,给出了部分过程如图所示.则这个两位数
”时,给出了部分过程如图所示.则这个两位数![]() 可能为_____.
可能为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂甲、乙两人加工同一种零件,每小时甲比乙多加工10个这种零件,甲加工150个这种零件所用的时间与乙加工120个这种零件所用的时间相等,
(1)甲、乙两人每小时各加工多少个这种零件?
(2)该工厂计划加工920个零件,甲参与加工这批零件不超过12天,则乙至少加工多少天才能加工完这批零件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下表记录了一名球员在罚球线上投篮的结果.
投篮次数(n) | 50 | 100 | 150 | 200 | 250 | 300 | 350 |
投中次数(m) | 28 | 60 | 78 | 104 | 123 | 152 | 251 |
投中频率( |
|
|
|
|
|
|
|
(1)计算表中的投中频率(精确到0.01);
(2)这名球员投篮一次,投中的概率约是多少(精确到0.1)?
查看答案和解析>>
科目:初中数学 来源: 题型:
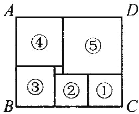
【题目】如图所示,是一块电脑屏幕上出现的矩形色块图,由6个颜色不同的正方形组成,设中间最小的一个正方形边长为1,则这个矩形的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
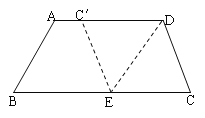
【题目】如图,在梯形纸片ABCD中,AD∥BC,AD>CD,将纸片沿过点D的直线折叠,使点C落在AD上的点C′处,折痕DE交BC于点E,连结C′E.
(1)求证:四边形ECDC′是菱形;
(2)若BC=CD+AD,试判断四边形ABED的形状,并加以证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com