
 ),E点坐标为(1,0),将△COE沿直线CE折叠,点O落在点D处.
),E点坐标为(1,0),将△COE沿直线CE折叠,点O落在点D处.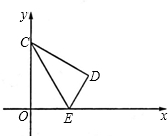 (1)求直线CE的解析式;
(1)求直线CE的解析式;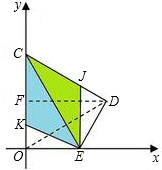 解:(1)设直线CE的解析式为y=kx+b(k≠0).
解:(1)设直线CE的解析式为y=kx+b(k≠0). ),E点坐标为(1,0),
),E点坐标为(1,0), ,
, ,b=
,b= ,即直线CE的解析式为y=-
,即直线CE的解析式为y=- x+
x+ ;
; ,
, OC=
OC= ,DF=
,DF= OF=
OF= ,
, ,
, );
); );②△KCE,点K(0,
);②△KCE,点K(0, ).
).

科目:初中数学 来源: 题型:
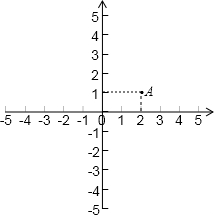 在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得△AOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,…,PK的坐标(有k个就标到PK为止,不必写出画法).
在平面直角坐标系内,已知点A(2,1),O为坐标原点.请你在坐标轴上确定点P,使得△AOP成为等腰三角形.在给出的坐标系中把所有这样的点P都找出来,画上实心点,并在旁边标上P1,P2,…,PK的坐标(有k个就标到PK为止,不必写出画法).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com