
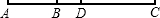 如图,已知线段AB=8,延长线段AB到C,使BC=2AB,点D是AC的中点.
如图,已知线段AB=8,延长线段AB到C,使BC=2AB,点D是AC的中点. 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:解答题
 解不等式组:$\left\{{\begin{array}{l}{\frac{1-2x}{3}≤x+2}\\{2x+2>2({2x-1})}\end{array}}\right.$.把它的解集在数轴上表示出来,并写出这个不等式组的整数解.
解不等式组:$\left\{{\begin{array}{l}{\frac{1-2x}{3}≤x+2}\\{2x+2>2({2x-1})}\end{array}}\right.$.把它的解集在数轴上表示出来,并写出这个不等式组的整数解.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
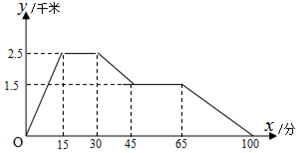 下面的图象反映的过程是:李华从家跑步去体育场,在那里锻炼了一阵后又走到书店去买书,然后散步走回家.其中x表示时间,y表示李华离家的距离.
下面的图象反映的过程是:李华从家跑步去体育场,在那里锻炼了一阵后又走到书店去买书,然后散步走回家.其中x表示时间,y表示李华离家的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com