
【题目】已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,抛物线
两点,抛物线![]() 经过
经过![]() 、
、![]() 两点,与
两点,与![]() 轴的另一个交点为
轴的另一个交点为![]() ,且
,且![]() .
.
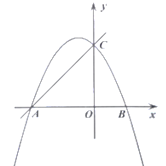
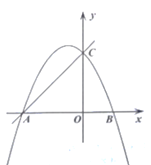
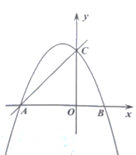
(1)求抛物线的解析式;
(2)点![]() 在
在![]() 上,点
上,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,点
,点![]() 为第一象限内的一点,当
为第一象限内的一点,当![]() 是以
是以![]() 为斜边的等腰直角三角形时,连接
为斜边的等腰直角三角形时,连接![]() ,设
,设![]() 的长度为
的长度为![]() ,
,![]() 的面积为
的面积为![]() ,请用含
,请用含![]() 的式子表示
的式子表示![]() ,并写出自变量
,并写出自变量![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,连接![]() 、
、![]() ,将
,将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置(
的位置(![]() 与
与![]() 对应),若
对应),若![]() ,求点
,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)
;(2)![]() (0<t<4);(3)K(1,-1)
(0<t<4);(3)K(1,-1)
【解析】
(1)利用![]() 求出点C、A的坐标及点B的坐标,即可代入
求出点C、A的坐标及点B的坐标,即可代入![]() 求出解析式;
求出解析式;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,设QF=m,根据△QDF≌△DPE 求出FD=4+t-m,EP=4-t+m,解出m=t ,即可根据三角形的面积公式计算得到函数解析式及t的取值范围;
(3)作PL∥OQ ,GM⊥AB于M ,KN⊥AB于N,证得 △PGL≌△QGC,得到GP=GQ,根据勾股定理求出t,再证明四边形PGDK为正方形,根据正方形的性质及△GMP≌△PNK求出AN及ON即可.
(1)解:当x=0时,y=4,∴C(0,4)
当y=0时,x=-4,∴A(-4,0)
∵OC=2OB,
∴OB=2 ,
∴B(2,0)
代入抛物线解析式得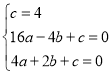 ,
,
解得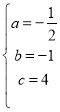 ,
,
∴抛物线的解析式为![]() ;
;
(2)过点D作DE⊥x轴于E,作QF⊥DE于F,
∴四边形QOEF为矩形
∴QF=OE,QO=FE,
设QF=m,
∵△QDF≌△DPE ,
∴QF=DE=m ,FD=EP,
∵FD=4+t-m,EP=4-t+m,
∴4-t+m=4+t-m,
∴m=t ,
∵OP=4-t,
∴![]() (0<t<4),
(0<t<4),
(3)作PL∥OQ ,GM⊥AB于M ,KN⊥AB于N,
∵OC=OA,
∴PL=PA ,
∵PA=CQ,
∴PL=CQ,
∴△PGL≌△QGC,
∴GP=GQ,
∵OG=![]() ,
,
∴PQ=![]() ,
,
在Rt△OPQ中,得(4-t)2+(4+t)2=![]() ,
,
∴t=2 ,
∵△PDG为等腰直角三角形,
∴四边形PGDK为正方形,
∵OQ=6,
∴GM=3,
∵GP=GO,
∴PM=MO=1,
∵△GMP≌△PNK,
∴GM=PN=3,PM=KN=1,
∴AN=5,ON=1,
∴K(1,-1)



 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
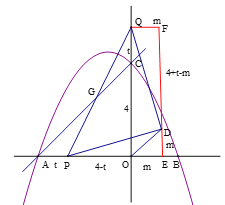
【题目】如图1,抛物线![]() 与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
与x轴交于A,B两点,与y轴交于点C,点D为线段AC的中点,直线BD与抛物线交于另一点E,与y轴交于点F.
(1)如图1,点P是直线BE上方抛物线上一动点,连接PD,PF,当△PDF的面积最大时,在线段BE上找一点G,使得PG﹣![]() EG的值最小,求出PG﹣
EG的值最小,求出PG﹣![]() EG的最小值;
EG的最小值;
(2)如图2,点M为抛物线上一点,点N在抛物线的对称轴上,点K为平面内一点,当以点A、M、N、K为顶点的四边形是正方形时,直接写出点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A,B的坐标分别为(4,0),(3,2).
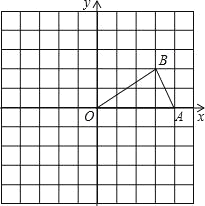
(1)画出△AOB关于原点O对称的图形△COD;
(2)将△AOB绕点O按逆时针方向旋转90°得到△EOF,画出△EOF;
(3)点D的坐标是 ,点F的坐标是 ,此图中线段BF和DF的关系是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】窑沟村对第一季度A、B两种水果的销售情况进行统计,两种水果的销售量如图所示.
(1)第一季度B种水果的月平均销售量是多少吨?
(2)一月A种水果的销售量是50吨,到三月A种水果的销售量是72吨,第一季度A种水果的销售量的月平均增长率相同,求二月A种水果销售了多少吨?
(3)根据以上信息,请将统计图补充完整.
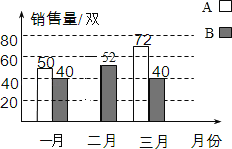
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小鸣想每天多做几套数学题,妈妈想通过一个游戏决定小鸣多做题的数量:在一个不透鸣的盒子中放入三张卡片,每张卡片上写着一个实数,分别为3,![]() ,2
,2![]() (每张卡片除了上面的实数不同以外其余均相同),妈妈让小鸣从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小鸣每天做五套,否则就多做十套.
(每张卡片除了上面的实数不同以外其余均相同),妈妈让小鸣从中任意取一张卡片,如果抽到的卡片上的数是有理数,就让小鸣每天做五套,否则就多做十套.
(1)请你直接写出按照妈妈的规则小鸣每天做五套数学题的概率;
(2)小鸣想和妈妈重新约定游戏规则:自己从盒子中随机抽取两次,每次抽取一张卡片,第一次抽取后记下卡片上的数,再将卡片放回盒中抽取第二次,如果抽取的两数之积是有理数,自己每天做五套数学题,否则每天做十套.用列表法或树状图法求按此规则小鸣每天做十套数学题的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,矩形ABCD中,E是AD的中点,以点E直角顶点的直角三角形EFG的两边EF,EG分别过点B,C,∠F=30°.
(1)求证:BE=CE
(2)将△EFG绕点E按顺时针方向旋转,当旋转到EF与AD重合时停止转动.若EF,EG分别与AB,BC相交于点M,N.(如图2)
①求证:△BEM≌△CEN;
②若AB=2,求△BMN面积的最大值;
③当旋转停止时,点B恰好在FG上(如图3),求sin∠EBG的值.
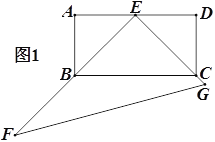
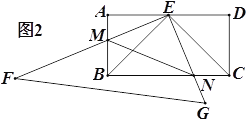
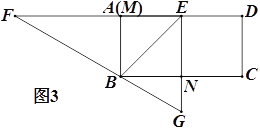
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD
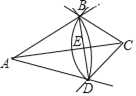
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,BC=2;
①求∠BAD所对的弧BD的长;②直接写出AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,E是AC上一点,且AE=AB,∠BAC=2∠EBC ,以AB为直径的⊙O交AC于点D,交EB于点F.
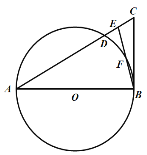
(1)求证:BC与⊙O相切;
(2)若AB=8,BE=4,求BC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线![]() 与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.
与y轴交于C点,与x轴交于A,B两点(点A在点B左侧),且点A的横坐标为-1.

(1)求a的值;
(2)设抛物线的顶点P关于原点的对称点为![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将抛物线在A,B两点之间的部分(包括A, B两点),先向下平移3个单位,再向左平移m(![]() )个单位,平移后的图象记为图象G,若图象G与直线
)个单位,平移后的图象记为图象G,若图象G与直线![]() 无交点,求m的取值范围.
无交点,求m的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com