
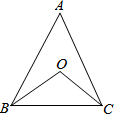
 如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )
如图,△ABC中,∠A=α°,BO、CO分别是∠ABC、∠ACB的平分线,则∠BOC的度数是( )| A. | 2α° | B. | (α+60)° | C. | (α+90)° | D. | ($\frac{1}{2}$α+90)° |
分析 根据三角形的内角和定理和角平分线的定义求出∠OBC+∠OCB的度数,再根据三角形的内角和等于180°,即可求出∠BOC的度数.
解答 解:∵∠A=α°,
∴∠ABC+∠ACB=180°-∠A=180°-α,
∵BO,CO分别是∠ABC,∠ACB的平分线,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×(180°-α)=90°-$\frac{1}{2}$α,
∴∠BOC=180°-(∠OBC+∠OCB)=180°-(90°-$\frac{1}{2}$α)=$\frac{1}{2}$α+90°.
故选:D
点评 本题主要利用三角形的内角和定理和角平分线的定义,熟练掌握定理和概念是解题的关键.


科目:初中数学 来源: 题型:解答题
 中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.
中日钓鱼岛争端持续,我海监船加大钓鱼岛海域的巡航维权力度.如图,OA⊥OB,OA=36海里,OB=12海里,钓鱼岛位于O点,我国海监船在点B处发现有一不明国籍的渔船,自A点出发沿着AO方向匀速驶向钓鱼岛所在地点O,我国海监船立即从B处出发以相同的速度沿某直线去拦截这艘渔船,结果在点C处截住了渔船.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 图象的开口向下 | B. | 图象的对称轴是直线x=-2 | ||
| C. | 函数最小值为1 | D. | 当x<2时,y随x的增大而增大 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com