
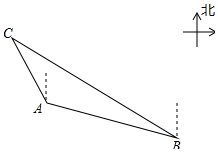
 如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号)
如图,一艘海上巡逻船在A地巡航,这时接到B地海上指挥中心紧急通知:在指挥中心北偏西60°向的C地,有一艘渔船遇险,要求马上前去救援.此时C地位于北偏西30°方向上,A地位于B地北偏西75°方向上,A、B两地之间的距离为16海里.求A、C两地之间的距离.(保留根号) 分析 过点B作BD⊥CA交CA延长线于点D,根据题意可得∠ACB和∠ABC的度数,然后根据三角形外角定理求出∠DAB的度数,已知AB=12海里,可求出BD、AD的长度,在Rt△CBD中,解直角三角形求出CD的长度,继而可求出A、C之间的距离.
解答 解:过点B作BD⊥CA交CA延长线于点D,
由题意得,∠ACB=60°-30°=30°,
∠ABC=75°-60°=15°,
∴∠DAB=∠DBA=45°,
在Rt△ABD中,AB=16海里,∠DAB=45°,
∴BD=AD=ABcos45°=8$\sqrt{2}$(海里),
在Rt△CBD中,CD=$\frac{BD}{tan30°}$=8$\sqrt{6}$,
∴AC=(8$\sqrt{6}$-8$\sqrt{2}$)(海里),
答:A、C两地之间的距离是8($\sqrt{6}$-$\sqrt{2}$)海里.
点评 本题考查了解直角三角形的知识,解答本题的关键是构造直角三角形,利用三角函数的知识求解相关线段的长度,难度一般.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
 如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm
如图在△ABC中,AD⊥BC于D点,正方形EFGH的一边FG在BC上,顶点E,H分别在AB,AC上,BC=40cm,AD=30cm查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
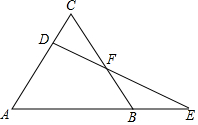 如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.
如图,已知△ABC是等边三角形,D为AC边上的一个动点,延长AB到E,使BE=CD,连结DE交BC于F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com