
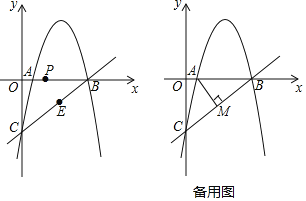
【题目】如图,抛物线![]() 经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为
经过x轴上的点A(1,0)和点B及y轴上的点C,经过B、C两点的直线为![]() .
.
①求抛物线的解析式.
②点P从A出发,在线段AB上以每秒1个单位的速度向B运动,同时点E从B出发,在线段BC上以每秒2个单位的速度向C运动.当其中一个点到达终点时,另一点也停止运动.设运动时间为t秒,求t为何值时,△PBE的面积最大并求出最大值.
③过点A作![]() 于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
于点M,过抛物线上一动点N(不与点B、C重合)作直线AM的平行线交直线BC于点Q.若点A、M、N、Q为顶点的四边形是平行四边形,求点N的横坐标.
【答案】①![]() ;②当
;②当![]() 时,△PBE的面积最大,最大值为
时,△PBE的面积最大,最大值为![]() ;③点N的横坐标为:4或
;③点N的横坐标为:4或![]() 或
或![]() .
.
【解析】
①点B、C在直线为![]() 上,则B(﹣n,0)、C(0,n),点A(1,0)在抛物线上,所以
上,则B(﹣n,0)、C(0,n),点A(1,0)在抛物线上,所以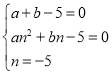 ,解得
,解得![]() ,
,![]() ,因此抛物线解析式:
,因此抛物线解析式:![]() ;
;
②先求出点P到BC的高h为![]() ,于是
,于是![]() ,当
,当![]() 时,△PBE的面积最大,最大值为
时,△PBE的面积最大,最大值为![]() ;
;
③由①知,BC所在直线为:![]() ,所以点A到直线BC的距离
,所以点A到直线BC的距离![]() ,过点N作x轴的垂线交直线BC于点P,交x轴于点H.设
,过点N作x轴的垂线交直线BC于点P,交x轴于点H.设![]() ,则
,则![]() 、
、![]() ,易证△PQN为等腰直角三角形,即
,易证△PQN为等腰直角三角形,即![]() ,
,![]() ,Ⅰ.
,Ⅰ.![]() ,所以
,所以![]() 解得
解得![]() (舍去),
(舍去),![]() ,Ⅱ.
,Ⅱ.![]() ,
,![]() 解得
解得![]() ,
,![]() (舍去),Ⅲ.
(舍去),Ⅲ.![]() ,
,![]() ,解得
,解得![]() (舍去),
(舍去),![]() .
.
解:①∵点B、C在直线为![]() 上,
上,
∴B(﹣n,0)、C(0,n),
∵点A(1,0)在抛物线上,
∴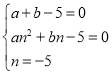 ,
,
∴![]() ,
,![]() ,
,
∴抛物线解析式:![]() ;
;
②由题意,得,
![]() ,
,![]() ,
,
由①知,![]() ,
,
∴点P到BC的高h为![]() ,
,
∴![]() ,
,
当![]() 时,△PBE的面积最大,最大值为
时,△PBE的面积最大,最大值为![]() ;
;
③由①知,BC所在直线为:![]() ,
,
∴点A到直线BC的距离![]() ,
,
过点N作x轴的垂线交直线BC于点P,交x轴于点H.
设![]() ,则
,则![]() 、
、![]() ,
,
易证△PQN为等腰直角三角形,即![]() ,
,
∴![]() ,
,
Ⅰ.![]() ,
,
∴![]()
解得![]() ,
,![]() ,
,
∵点A、M、N、Q为顶点的四边形是平行四边形,
∴![]() ;
;
Ⅱ.![]() ,
,
∴![]()
解得![]() ,
,![]() ,
,
∵点A、M、N、Q为顶点的四边形是平行四边形,
![]() ,
,
∴![]() ,
,
Ⅲ.![]() ,
,
∴![]() ,
,
解得![]() ,
,![]() ,
,
∵点A、M、N、Q为顶点的四边形是平行四边形,
![]() ,
,
∴![]() ,
,
综上所述,若点A、M、N、Q为顶点的四边形是平行四边形,点N的横坐标为:4或![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
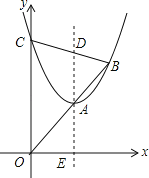
【题目】如图,抛物线y=x2+bx+c(c>0)与y轴交于点C,顶点为A,抛物线的对称轴交x轴于点E,交BC于点D,tan∠AOE=![]() .直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
.直线OA与抛物线的另一个交点为B.当OC=2AD时,c的值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某电信公司提供了A,B两种方案的移动通讯费用y(元)与通话时间x(元)之间的关系,则下列结论中正确的有( )
(1)若通话时间少于120分,则A方案比B方案便宜20元;
(2)若通话时间超过200分,则B方案比A方案便宜12元;
(3)若通讯费用为60元,则B方案比A方案的通话时间多;
(4)若两种方案通讯费用相差10元,则通话时间是145分或185分.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列10×10的网格中,横、纵坐标均为整数的点叫做格点,例如A(3,0),B(4,3)都是格点.将△AOB绕点O顺时针旋转90°得到△COD(点A,B的对应点分别为点C,D).
(1)作出△COD;
(2)下面仅用无刻度的直尺画△AOD的内心I,操作如下:
第一步:在x轴上找一格点E,连接DE,使OE=OD;
第二步:在DE上找一点F,连接OF,使OF平分∠AOD;
第三步:找格点G,得到正方形OAGC,连接AC,则AC与OF的交点I是△OAD的内心.
请你按步骤完成作图,并直接写出E,F,I三点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为5的⊙O中,弦AB=8,P是弦AB所对的优弧上的动点,连接AP,过点A作AP的垂线交射线PB于点C,当△PAB是等腰三角形时,线段BC的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】吉祥超市准备购进甲、乙两种绿色袋装食品共800袋.甲、乙两种绿色袋装食品的进价和售价如表.已知:用2000元购进甲种袋装食品的数量与用1600元购进乙种袋装食品的数量相同.
甲 | 乙 | |
进价(元/袋) | m | m﹣2 |
售价(元/袋) | 20 | 13 |
(1)求m的值;
(2)假如购进的甲、乙两种绿色袋装食品全部卖出,所获总利润不少于5200元,且不超过5280元,问该超市有几种进货方案?(利润=售价﹣进价)
查看答案和解析>>
科目:初中数学 来源: 题型:
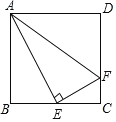
【题目】如图,在正方形ABCD中,E是BC的中点,F是CD上一点,AE⊥EF.有下列结论:①∠BAE=30°;②射线FE是∠AFC的角平分线;③AE2=ADAF;④AF=AB+CF.其中正确结论为是______.(填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,AB=AC,把△ABC绕A点沿顺时针方向旋转得到△ADE,连接BD,CE交于点F.

(1)求证:△AEC≌△ADB;(2)若AB=2,∠BAC=45°,当四边形ADFC是菱形时,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】课外阅读是提高学生素养的重要途径.某中学为了了解全校学生课外阅读情况,随机抽查了200名学生,统计他们平均每天课外阅读时间(小时).根据每天课外阅读时间的长短分为A,B,C.D四类,下面是根据所抽查的人数绘制的两幅不完整的统计图表,请根据图中提供的信息,解答下面的问题:
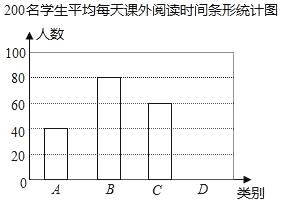
200名学生平均每天课外阅读时间统计表
类别 | 时间t(小时) | 人数 |
A | t<0.5 | 40 |
B | 0.5≤t<1 | 80 |
C | 1≤t<1.5 | 60 |
D | t≥1.5 | a |
(1)求表格中a的值,并在图中补全条形统计图:
(2)该校现有1800名学生,请你估计该校共有多少名学生课外阅读时间不少于1小时?
(3)请你根据上述信息对该校提出相应的建议
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com