
【题目】已知:如图,AD是△ABC的中线,∠ACE是△ABC的外角. 
(1)读下列语句,尺规作图,保留作图痕迹. ①作∠ACE的角平分线,交BA延长线于点F;
②过点D作DH∥AC,交AB于点H,连接CH.
(2)依据以上条件,解答下列问题. ①与△AHD面积相等的三角形是;
②若∠B=40°,∠F=30°,求∠BAC的度数.
【答案】
(1)解:如图所示,
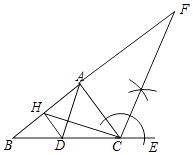
(2)△BDH,△CDH;100°
【解析】解:(2)①∵AC∥DH, ∴△CDH与△AHD面积相等,
∵D是BC的中点,AC∥DH,
∴H是AB的中点,
∴△BDH与△AHD面积相等,
所以答案是:△BDH,△CDH;
②∵∠BAC是△AFC的外角,
∴∠BAC=∠ACF+∠F,
∵∠FCE是△BFC的外角,
∴∠FCE=∠B+∠F,
∵CF是∠ACE的角平分线,
∴∠FCE=∠ACF,
∴∠BAC=∠ACF+∠F=∠FCE+∠F=∠B+∠F+∠F=40°+30°+30°=100°
【考点精析】本题主要考查了平行线的性质和角平分线的性质定理的相关知识点,需要掌握两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补;定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上才能正确解答此题.


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线 ![]() 经过点
经过点 ![]() ,交y 轴于点C:
,交y 轴于点C:
(1)求抛物线的解析式(用一般式表示).
(2)点 ![]() 为
为 ![]() 轴右侧抛物线上一点,是否存在点
轴右侧抛物线上一点,是否存在点 ![]() 使
使 ![]() ,若存在请直接给出点
,若存在请直接给出点 ![]() 坐标;若不存在请说明理由.
坐标;若不存在请说明理由.
(3)将直线 ![]() 绕点
绕点 ![]() 顺时针旋转
顺时针旋转 ![]() ,与抛物线交于另一点
,与抛物线交于另一点 ![]() ,求
,求 ![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一个隧道的横断面,它的形状是以点O为圆心的圆的一部分,如果圆的半径为 ![]() m,弦CD=4m,那么隧道的最高处到CD的距离是( )
m,弦CD=4m,那么隧道的最高处到CD的距离是( ) 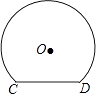
A.![]() m
m
B.4m
C.![]() m
m
D.6m
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表: 
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了对学生进行爱国主义教育,某校组织学生去看演出,有甲乙两种票,已知甲乙两种票的单价比为4:3,单价和为42元.
(1)甲乙两种票的单价分别是多少元?
(2)学校计划拿出不超过750元的资金,让七年级一班的36名学生首先观看,且规定购买甲种票必须多于15张,有哪几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【阅读新知】
三角形中任何一边的平方等于其它两边的平方的和减去这两边与它们的夹角的余弦的积的两倍.
即:如图1,.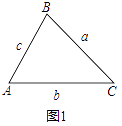
在△ABC中,已知AB=c,BC=a,CA=b,则有:
a2=b2+c2﹣2bccosA,b2=a2+c2﹣2accosB,c2=a2+b2﹣2abcosC
利用这个正确结论可求解下列问题:
例在△ABC中,已知a=2 ![]() ,b=2
,b=2 ![]() ,c=
,c= ![]() ,求∠A.
,求∠A.
解:∵a2=b2+c2﹣2bccosA,
cosA= ![]() =
= ![]() =
= ![]() .
.
∴∠A=60°.
【应用新知】
(1)选择题:在△ABC中,已知b=ccosA,a=csinB,那么△ABC是( ).
A.等边三角形
B.等腰三角形
C.等腰直角三角形
D.直角三角形
(2)如图2,
某客轮在A处看港口D在客轮的北偏东50°,A处看灯塔B在客轮的北偏西30°,距离为2 ![]() 海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
海里,客轮由A处向正北方向航行到C处时,再看港口D在客轮的南偏东80°,距离为6海里.求此时C处到灯塔B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点G为BC边的中点,点H在AF上,动点P以每秒1cm的速度沿图1的边运动,运动路径为![]() ,相应的
,相应的![]() 的面积
的面积![]() 关于运动时间
关于运动时间![]() 的函数图象如图2,若
的函数图象如图2,若![]() ,则下列结论正确的个数有
,则下列结论正确的个数有![]()
![]()
![]() 图1中BC长4cm;
图1中BC长4cm;![]() 图1中DE的长是3cm;
图1中DE的长是3cm;![]() 图2中点M表示4秒时的y值为
图2中点M表示4秒时的y值为![]() ;
;![]() 图2中的点N表示12秒时y值为
图2中的点N表示12秒时y值为![]() .
.

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程:
O是直线AB上一点,∠COD = 90°,OE平分∠BOC.
(1)如图1,若∠ AOC = 50°,求∠DOE的度数;
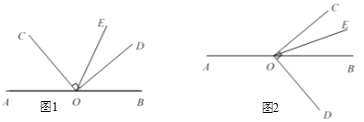
解:∵O是直线AB上一点,
∴∠AOC +∠BOC =180°.
∵∠AOC =50°,
∴∠BOC =130°.
∵OE平分∠BOC(已知),
∴∠COE =![]() ∠BOC ( ).
∠BOC ( ).
∴∠COE = °.
∵∠COD = 90°,∠DOE =∠ ∠ ,
∴∠DOE = °.
(2)将图1中∠ COD按顺时针方向转至图2所示的位置,OE仍然平分∠BOC.试猜想∠AOC与∠DOE的度数之间的关系为: .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com