
【题目】如图所示,反映的是九(1)班学生外出乘车、步行、骑车的人数直方图的一部分和圆形分布图,下列说法:①九(1)班外出步行有8人;②在圆形统计图中,步行人数所占的圆心角度数为82°;
③九(1)班外出的学生共有40人;④若该校九年级外出的学生共有500人,那么估计全年级外出骑车的人约有150人,其中正确的结论是( )


A. ①②③ B. ①③④ C. ②③ D. ②④
科目:初中数学 来源: 题型:
【题目】为了解学生整体的数学学习能力,年级组织了“数学钻石活动”,从中随机抽取部分学生的成绩进行统计分析,整理得到如下不完整的频数分布表和数分布直方图:


(1)表中的![]() ,
,![]() ;
;
(2)把上面的频数分布直方图补充完整;
(3)根据调查结果,估计年级500名学生中,成绩不低于85分的人数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)填写下表,并观察下列两个代数式的值的变化情况。

(2)随着n的值逐渐变大,两个代数式的值如何变化?
(3)估计一下,哪个代数式的值先超过100?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:
如图1所示的图形,像我们常见的学习用品--圆规.我们不妨把这种图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?请解决以下问题:
(1)观察“规形图”,试探究∠BPC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下问题:
①如图2:已知△ABC,BP平分∠ABC,CP平分∠ACB,直接写出∠BPC与∠A之间存在的等量关系为: .
迁移运用:如图3:在△ABC中,∠A=80°,点O是∠ABC,∠ACB角平分线的交点,点P是∠BOC,∠OCB角平分线的交点,若∠OPC=100°,则∠ACB的度数 .
②如图4:若D点是△ABC内任意一点,BP平分∠ABD,CP平分∠ACD.直接写出∠BDC、∠BPC、∠A之间存在的等量关系为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家知道![]() 是无理数,而无理数是无限不循环小数,因此
是无理数,而无理数是无限不循环小数,因此![]() 的小数部分我们不可能全部写出来,
的小数部分我们不可能全部写出来,![]() ,于是可用
,于是可用![]() 来表示
来表示![]() 的小数部分.请解答下列问题:
的小数部分.请解答下列问题:
(1)![]() 的整数部分是________,小数部分是________.
的整数部分是________,小数部分是________.
(2)如果![]() 的小数部分为
的小数部分为![]() ,
,![]() 的整数部分为
的整数部分为![]() ,求
,求![]() 的值.
的值.
(3)已知:![]() ,其中
,其中![]() 是整数,且
是整数,且![]() ,求
,求![]() 的相反数.
的相反数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为菱形,E为对角线AC上的一个动点,连结DE并延长交射线AB于点F,连结BE.
(1)求证:∠AFD=∠EBC;
(2)若∠DAB=90°,当△BEF为等腰三角形时,求∠EFB的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
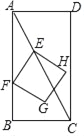
【题目】如图,在矩形ABCD中,AB=4,BC=2,点E从点A出发,以每秒![]() 个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
个单位长度的速度沿对角线AC向终点C运动,点F从点B出发,以每秒2个单位长度的速度沿边BA向终点A运动,连结EF,将线段EF绕点F顺时针旋转90°得到线段FG,以EF,FG为边作正方形EFGH,设点E运动的时间为t秒(t>0).
(1)用含t的代数式表示点E到边AB的距离.
(2)当点G落在边AB上时,求t的值.
(3)连结BG,设△BFG的面积为S平方单位(S>0),求S与t之间的函数关系式.
(4)直接写出当正方形EFGH的顶点与点B,D距离相等时的t值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知∠AOB=30°,点P在∠AOB的内部,P1与P关于OA对称,P2与P关于OB对称,则△P1OP2是
A. 含30°角的直角三角形 B. 顶角是30的等腰三角形
C. 等边三角形 D. 等腰直角三角形
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=90°,AD=CD+AB,∠BAC=45°,E是BC上一点,且∠DAE=45°,若BC=8,则△ADE面积为__.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com