
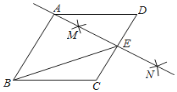
【题目】如图,在菱形![]() 中,
中,![]() ,按以下步骤作图:①分别以点
,按以下步骤作图:①分别以点![]() 和点
和点![]() 为圆心,为圆心,大于号
为圆心,为圆心,大于号![]() 的长为半径面狐,两弧交于点
的长为半径面狐,两弧交于点![]() ,
,![]() :②做直线
:②做直线![]() ,且
,且![]() 恰好经过点
恰好经过点![]() ,与
,与![]() 交于点
交于点![]() ,连接
,连接![]() ,则
,则![]() 的值为( )
的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
科目:初中数学 来源: 题型:
【题目】如图,正方形![]() 中,
中,![]() ,
,![]() 是
是![]() 边的中点,点
边的中点,点![]() 是正方形内一动点,
是正方形内一动点,![]() ,连接
,连接![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 得
得![]() ,连接
,连接![]() ,
,![]() .
.
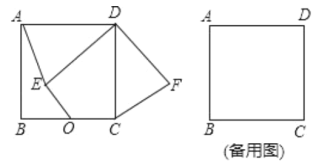
(1)求证:![]() ;
;
(2)若![]() ,
,![]() ,
,![]() 三点共线,连接
三点共线,连接![]() ,求线段
,求线段![]() 的长.
的长.
(3)求线段![]() 长的最小值.
长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
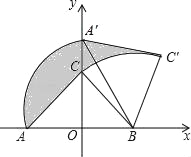
【题目】如图,Rt△ABC中,∠ACB=90°,AC=BC,在以AB的中点O为坐标原点,AB所在直线为x轴建立的平面直角坐标系中,将△ABC绕点B顺时针旋转,使点A旋转至y轴的正半轴上的点A′处,若AO=OB=2,则阴影部分面积为( )
A. πB. ![]() π﹣1C.
π﹣1C. ![]() +1D.
+1D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,AB为⊙O的直径,弦CD⊥AB于点E,在CD的延长线上取一点P,PG与⊙O相切于点G,连接AG交CD于点F.
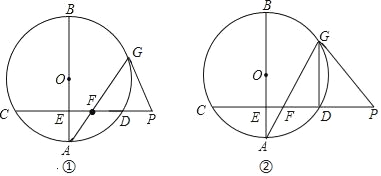
(Ⅰ)如图①,若∠A=20°,求∠GFP和∠AGP的大小;
(Ⅱ)如图②,若E为半径OA的中点,DG∥AB,且OA=2![]() ,求PF的长.
,求PF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)尝试探究
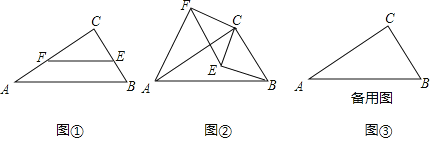
如图①,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 、
、![]() 分别是边
分别是边![]() 、
、![]() 上的点,且
上的点,且![]() .
.
①![]() 的值为多少;②直线
的值为多少;②直线![]() 与直线
与直线![]() 的位置关系;
的位置关系;
(2)类比延伸
如图②,若将图①中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,
,![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直线
与直线![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(3)拓展运用
若![]() ,
,![]() ,在旋转过程中,当
,在旋转过程中,当![]() ,
,![]() ,
,![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 尝试探究
尝试探究
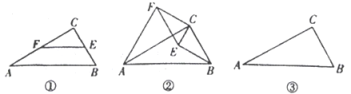
如图-![]() ,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
,在△ABC中,∠C=90°,∠A=30°,点E、F分别是BC、AC边上的点,且EF//BC.
![]()
![]() 的值为 ;
的值为 ;![]() 直线
直线![]() 与直线
与直线![]() 的位置关系为 ;
的位置关系为 ;
![]() 类比延伸
类比延伸
如图![]() ,若将图
,若将图![]() 中的
中的![]() 绕点
绕点![]() 顺时针旋转,连接
顺时针旋转,连接![]() ,则在旋转的过程中,请判断
,则在旋转的过程中,请判断![]() 的值及直线
的值及直线![]() 与直
与直![]() 线的位置关系,并说明理由;
线的位置关系,并说明理由;
![]() 拓展运用
拓展运用
若![]() ,在旋转过程中,当
,在旋转过程中,当![]() 三点在同一直线上时,请直接写出此时线段
三点在同一直线上时,请直接写出此时线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB = 90°,BC = 3,AC = 4,点D为边AB上一点.将△BCD沿直线CD翻折,点B落在点E处,联结AE.如果AE // CD,那么BE =________.

查看答案和解析>>
科目:初中数学 来源: 题型:
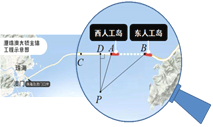
【题目】2018年10月23日,港珠澳大桥正式开通,成为横亘在伶仃洋上的一道靓丽的风景.大桥主体工程隧道的东、西两端各设置了一个海中人工岛,来衔接桥梁和海底隧道,西人工岛上的A点和东人工岛上的B点间的距离约为5.6千米,点C是与西人工岛相连的大桥上的一点,A,B,C在一条直线上.如图,一艘观光船沿与大桥![]() 段垂直的方向航行,到达P点时观测两个人工岛,分别测得
段垂直的方向航行,到达P点时观测两个人工岛,分别测得![]() 与观光船航向
与观光船航向![]() 的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离
的夹角∠DPA=18°,∠DPB=53°,求此时观光船到大桥AC段的距离![]() 的长.
的长.
参考数据:![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() ,
,![]() °
°![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com