
【题目】如图,四边形ABCD是平行四边形,以AB为直径的⊙0经过点D,E是⊙O上一点,且∠AED=45°,

(1)求证:CD是⊙O的切线.
(2)若⊙O的半径为3,AE=5,求∠DAE的正弦值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)连结OD,如图,根据圆周角定理得到∠AOD=2∠AED=90°,则OD⊥AB,再利用平行四边形的性质得CD∥AB,所以OD⊥CD,于是根据切线的判定定理得到CD是⊙O的切线;
(2)连结BE,通过圆周角定理将∠ADE的正弦值转化为∠ABE的正弦值.
试题解析:(1)证明:连结OD,如图,

∵∠AOD=2∠AED=2×45°=90°,
∴OD⊥AB,
∵四边形ABCD是平行四边形,
∴CD∥AB,
∴OD⊥CD,
∴CD是⊙O的切线;
(2)解:连结BE,
∵AB为直径,
∴∠AEB=90°,
根据圆周角定理:∠ADE=∠ABE,
∴sin∠ADE=sin∠ABE=![]() .
.
即∠DAE的正弦值是![]() .
.


 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】某商场销售一批进价为10元的新商品,为寻求合适的销售价格,他们进行了4天的试销,试销情况如下表:
第1天 | 第2天 | 第3天 | 第4天 | |
日销售单价x(元) | 20 | 30 | 40 | 50 |
日销售量y(个) | 300 | 200 | 150 | 120 |
(1)根据试销情况,请你猜测并求出y与x之间的函数关系式;
(2)若该商场计划每天销售这种商品的利润要达到3600元,问该商品销售单价应定为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形网格中,建立如图所示的平面直角坐标系xOy,△ABC的三个顶点都在格点上,点A的坐标(4,4),请解答下列问题:
(1)画出△ABC关于y轴对称的△A1B1C1,并写出点A1、B1、C1的坐标;
(2)将△ABC绕点C逆时针旋转90°,画出旋转后的△A2B2C2,并求出点A到A2的路径长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天课间,顽皮的小明同学拿着老师的等腰三角板玩,不小心掉到两根柱子之间,如图所示,这一幕恰巧被数学老师看见了,于是有了下面这道题.
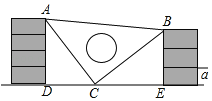
(1)求证:△ADC≌△CEB;
(2)如果每块砖的厚度a=10cm,请你帮小明求出三角板ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图正方形ABCD中,点E、F分别在CD、BC边上,△AEF是等边三角形.以下结论:①EC=FC;②∠AED=75°;③AF=![]() CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.
CE;④EF的垂直平分线是直线AC.正确结论个数有( )个.

A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
我们知道|x|的几何意义是:在数轴上数x对应的点与原点O的距离,这个结论可以推广为:|x1﹣x2|表示在数轴上数x1,x2对应点之间的距离.
例:解方程|x﹣1|+|x+2|=5.
由绝对值的几何意义知,该方程表示:求在数轴上与1和﹣2的距离之和为5的点对应的数,而在数轴上,1和﹣2的距离为|1﹣(﹣2)|=3,满足方程的x对应点在1的右边或﹣2的左边,若x对应点在1的右边,
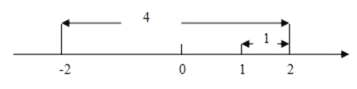
由图可知看出x=2;同理,若x对应点在﹣2的左边,可得x=﹣3,故原方程的解是x=2或x=﹣3.
参考阅读材料,解答下列问题:
(1)方程|x﹣2|+|x+3|=7的解为 .
(2)代数式|x﹣1|+|x+4|的最小值为 .
(3)如图,点A、B、C是数轴上的三点,A点表示数是-3,B点表示数是-1,C点表示数是6,点A,B,C开始在数轴上运动,若点A以每秒1个单位长度的速度向左运动,同时,点B和点C分别以每秒2个单位长度和3个单位长度的速度向右运动,假设t秒钟过后,若点A与点B之间的距离表示为AB,点A与点C之间的距离表示为AC,点B与点C之间的距离表示为BC.则AB= ,AC= .(用含t的代数式表示)
![]()
(4)在(3)的条件下,若mAC﹣4AB的值不随着时间t的变化而改变,试确定m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点E在△ABC的外部,点D边BC上,DE交AC于点F,若∠1=∠2,AE=AC,BC=DE.
(1)求证:AB=AD;
(2)若∠1=60°,判断△ABD的形状,并说明理由.
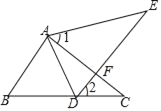
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B两处出发,沿轨道到达C处,B在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为d1,d2,则d1,d2与t的函数关系如图,试根据图象解决下列问题:
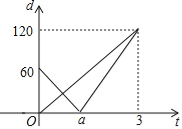
(1)填空:乙的速度v2= 米/分;
(2)写出d1与t的函数关系式:
(3)若甲、乙两遥控车的距离超过10米时信号不会产生相互干扰,试探求什么时间两遥控车的信号不会产生相互干扰?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com