
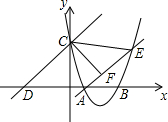
 如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.
如图,已知抛物线经过点A(2,0)和B(t,0)(t≥2),与y轴交于点C,直线l:y=x+2t经过点C,交x轴于点D,直线AE交抛物线于点E,且有∠CAE=∠CDO,作CF⊥AE于点F.分析 (1)求出点C,D的坐标,得到OC=OD,即可解答;
(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,利用已知条件证明△FGA≌△FHC,得到FH=FG,HC=AG,设F(m,m)则2t-m=m-2,求出m的值,即可解答;
(3)如图2,作ET⊥HF于T,分别得到E的横坐标是$\frac{{t}^{2}+1}{t-1}$,CH=t-1,FT=$\frac{2}{t-1}$,再由△HCF∽△TFE,得到$\frac{CH}{FT}=\frac{CF}{EF}$,即$\frac{(t-1)^{2}}{2}=\frac{CF}{EF}$,分类讨论:当△OBC∽△FEC时;当△OBC∽△FCE时;求出t的值,即可解答.
解答 解:(1)∵直线l:y=x+2t与y轴点C,交x轴于点D,
∴C(0,2t),D(-2t,0)
∴OC=OD,
∵∠COD=90°,
∴∠CDO=∠DCO=45°.
(2)如图1,作FG⊥x轴于点G,FH⊥y轴于点H,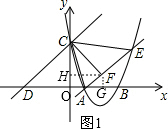
∵∠HOG=∠OGF=∠FHO=90°,
∴四边形OGFH是矩形
∴∠HFG=90°,
∴∠HFA+∠AFG=90°
又∵CF⊥AE,
∴∠CFH+∠HFA=90°
∴∠CFH=∠AFG,
又∵∠CAE=∠CDO=45°,
∴∠FCA=45°,
∴CF=AF,
又∵∠FGA=∠CHF=90°,
在△FGA和△FHC中,
$\left\{\begin{array}{l}{∠CHF=∠FGA}\\{∠CFH=∠AFG}\\{CF=AF}\end{array}\right.$
∴△FGA≌△FHC,
∴FH=FG,HC=AG,
设F(m,m)
则2t-m=m-2,
得m=t+1,
∴F(t+1,t+1).
(3)∵S△COD-S四边形COAF=S△COD-S正方形HOGF=7
∴$\frac{1}{2}(2t)^{2}-(t+1)^{2}$=7,
解得:t=4或-2(舍去),
则A点坐标(2,0),B点坐标(4,0),C点坐标(0,8)
设y=a(x-2)(x-4),
把C(0,8)代入y=a(x-2)(x-4),
解得a=1,
∴y=(x-2)(x-4)=x2-6x+8.
(4)t=3或2.
如图2,作ET⊥HF于T,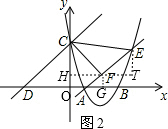
求得:E的横坐标是$\frac{{t}^{2}+1}{t-1}$,CH=t-1,FT=$\frac{2}{t-1}$,
由△HCF∽△TFE,
则$\frac{CH}{FT}=\frac{CF}{EF}$,
得:$\frac{(t-1)^{2}}{2}=\frac{CF}{EF}$
当△OBC∽△FEC时,$\frac{OC}{OB}=\frac{CF}{EF}$=2,
即$\frac{(t-1)^{2}}{2}$=2,
解得:t=3或t=-1( 舍去),
当△OBC∽△FCE时,$\frac{OB}{OC}=\frac{CF}{EF}=\frac{1}{2}$,
即$\frac{(t-1)^{2}}{2}=\frac{1}{2}$,
解得:t=2或t=0(舍去).
∴t=3或2.
点评 本题考查了二次函数的性质、全等三角形的性质定理与判定定理、相似三角形的性质定理与判定定理,解决本题的关键是作出辅助线,构建全等三角形、相似三角形,并进行分类讨论.


科目:初中数学 来源: 题型:选择题
| 成绩(分) | 6 | 7 | 8 | 9 | 10 |
| 人数 |  | 正 一 | 正 正 一 | 正 正  | 正 |
| A. | 9,8 | B. | 9,8.5 | C. | 8,8 | D. | 8,8.5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 158,158 | B. | 158,162 | C. | 162,160 | D. | 160,160 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
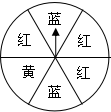 如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是( )
如图,一个可以自由转动的转盘被等分成6个扇形区域,并涂上了相应的颜色,转动转盘,转盘停止后,指针指向红色区域的概率是( )| A. | $\frac{2}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
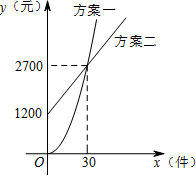 某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:
某公司推销一种产品,公司付给推销员的月报酬有两种方案如图所示:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 0个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com