
【题目】综合题。
(1)计算:4sin60°+|3﹣ ![]() |﹣(
|﹣( ![]() )﹣1+(π﹣2017)0 .
)﹣1+(π﹣2017)0 .
(2)解方程组: ![]() .
.
【答案】
(1)解:原式=4× ![]() +2
+2 ![]() ﹣3﹣2+1
﹣3﹣2+1
=4 ![]() ﹣4;
﹣4;
(2)解: ![]()
①+②×5得:13x=13,
解得:x=1,
把x=1代入②得:2﹣y=1,
解得:y=1,
所以原方程组的解为: ![]() .
.
【解析】(1)根据零指数幂,负整数指数幂,绝对值,特殊角的三角函数值分别请求出每一部分的值,再求出即可;(2)①+②×5得出13x=13,求出x,把x=1代入②求出y即可.
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本,需要知道零次幂和负整数指数幂的意义: a0=1(a≠0);a-p=1/ap(a≠0,p为正整数);aman=am+n(m、n是正整数);(am)n=amn(m、n是正整数);(ab)n=anbn(n是正整数);am/an=am-n(a不等于0,m、n为正整数);(a/b)n=an/bn(n为正整数).


科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD,AB=6,点E在边CD上,CE=2DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF,下列结论:①△ABG≌△AFG;②BG=GC;③EG=DE+BG;④AG∥CF;⑤S△FCA=3.6,其中正确结论是 . 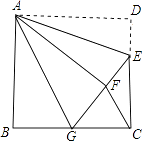
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明所在的学校加强学生的体育锻炼,准备从某体育用品商店一次购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),若购买2个篮球和3个足球共需310元,购买5个篮球和2个足球共需500元.
(1)每个篮球和足球各需多少元?
(2)根据实际情况,需从该商店一次性购买篮球和足球功60个,要求购买篮球和足球的总费用不超过4000元,那么最多可以购买多少个篮球?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在扇形AOB中,∠AOB=90°,正方形CDEF的顶点C是弧AB的中点,点D在OB上,点E在OB的延长线上,当正方形CDEF的边长为2时,阴影部分的面积为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx﹣2经过点A(1,0)和点B(4,0),与y轴交于点C.
附:阅读材料
法国弗朗索瓦韦达最早发现一元二次方程中根与系数的关系为:两根之和等于一次项系数与二次项系数之比的相反数,两根之积等于常数项羽二次项系数之比,人们称之为韦达定理.
即:设一元二次方程ax2+bx+c=0的两根为x1、x2 , 则:x1+x2=﹣ ![]() ,x1x2=
,x1x2= ![]() 能灵活运用韦达定理,有时可以使解题更为简单.
能灵活运用韦达定理,有时可以使解题更为简单.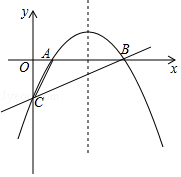
(1)求抛物线的解析式;
(2)以点A为圆心,作于直线BC相切的⊙A,求⊙A的面积;
(3)将直线BC向下平移n个单位后与抛物线交于点M、N,且线段MN=2CB,求直线MN的解析式及平移距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线l与抛物线y=mx2+nx相交于A(1,3 ![]() ),B(4,0)两点.
),B(4,0)两点.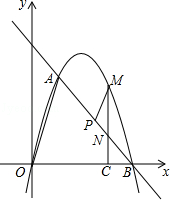
(1)求出抛物线的解析式;
(2)在坐标轴上是否存在点D,使得△ABD是以线段AB为斜边的直角三角形?若存在,求出点D的坐标;若不存在,说明理由;
(3)点P是线段AB上一动点,(点P不与点A、B重合),过点P作PM∥OA,交第一象限内的抛物线于点M,过点M作MC⊥x轴于点C,交AB于点N,若△BCN、△PMN的面积S△BCN、S△PMN满足S△BCN=2S△PMN , 求出 ![]() 的值,并求出此时点M的坐标.
的值,并求出此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=kx+2与x轴、y轴分别交于点A(﹣1,0)和点B,与反比例函数y= ![]() 的图象在第一象限内交于点C(1,n).
的图象在第一象限内交于点C(1,n). 
(1)求k的值;
(2)求反比例函数的解析式;
(3)过x轴上的点D(a,0)作平行于y轴的直线l(a>1),分别与直线AB和双曲线y= ![]() 交于点P、Q,且PQ=2QD,求点D的坐标.
交于点P、Q,且PQ=2QD,求点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一种某小区的两幢10层住宅楼间的距离为AC=30m,由地面向上依次为第1层、第2层、…、第10层,每层高度为3m.假设某一时刻甲楼在乙楼侧面的影长EC=h,太阳光线与水平线的夹角为α. 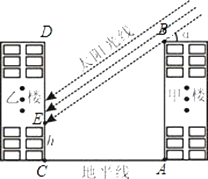
(1)用含α的式子表示h(不必指出α的取值范围);
(2)当α=30°时,甲楼楼顶B点的影子落在乙楼的第几层?若α每小时增加15°,从此时起几小时后甲楼的影子刚好不影响乙楼采光?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com