
| A. | 8 | B. | 4 | C. | 2 | D. | 1 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
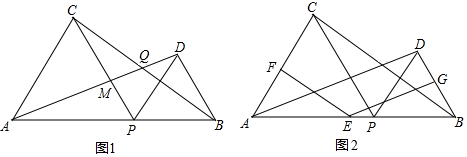
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
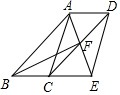 四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
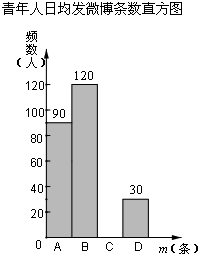 在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下:
在某项针对18-35岁的青年人每天发微博数量的调查中,设一个人的“日均发微博条数”为m,规定:当0≤m<5时为A级,5≤m<10时为B级,10≤m<15时为C级,m≥15时为D级.现随机抽取部分符合年龄条件的青年人开展每人“日均发微博条数”的调查,制作图表如下:| m | 频数 | 百分数 |
| A级(0≤m<5) | 90 | 0.3 |
| B级(5≤m<10) | 120 | a |
| C级(10≤m<15) | b | 0.2 |
| D级(m≥15) | 30 | 0.1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com